PDF version

Our normal number system is a positional system, where the position (column) of a digit represents its value. Starting from the right, we have the ones column, tens column, hundreds, thousands, and so on. Thus the number 3724 stands for three THOUSAND, seven HUNDRED, two TENS (called twenty), and four ONES.

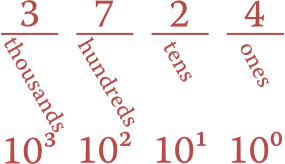
The columns in base ten

The values of those columns derive from the powers of ten, which is then called the base of the number system. The base ten number system is also called decimal.

There is nothing special about base ten, except that it’s what you learned from a young age. A positional numbering system can use any quantity as its base. Let’s take, for example, base five. In base five, the columns represent the quantities (from right to left) one, five, twenty-five, and a hundred twenty-five. We need to use five symbols to indicate quantities from zero up to four. For simplicity, let’s keep the same numerals we know: 0, 1, 2, 3, and 4.

The columns in base five

The number shown in this figure, 3104 in base five, represents the same quantity that we usually write as 404 in base ten. That’s because it is three × one hundred twenty-five (= 375), plus one × twenty-five (= 25) plus four ones (= 4), so 375 + 25 + 4 = 404.

You can count directly in base five; it looks like this: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100. (Those correspond to quantities from zero to twenty-five.)

You should try counting and converting between other bases. Below is an interesting video overview of the dozenal (base twelve) number system.

@wirehead2501 on Twitter

There is a relatively simple algorithm for converting from base ten to any foreign base. Suppose we have the number 344 (three hundred forty-four) that we’d like to write in base five.

We start by dividing the number by the desired base, so 344 ÷ 5 = 68.8. It helps to think of that as 68 with a remainder of 4. (The .8 corresponds to a remainder of 4 because .8 × 5 = 4.) Remember the remainder, but proceed with the whole-number part. So now we divide 68 ÷ 5 = 13.6 which is remainder 3. Next, 13 ÷ 5 = 2.6, again remainder 3. Finally, 2 ÷ 5 = 0.4, which is remainder 2.

We stop when the whole-number part becomes zero, and then write the remainders from right to left: 2334. Thus, 344 in base ten is written as ‘2334’ in base 5.

Summary questions

1. Convert the following base-five numbers into base ten. The first one is done for you.

   1. We take those digits and write them on top of the base-five column values, from right to left. Then we multiply the digit in each column (above the line) with the value of that column (below the line), and add the results.

      

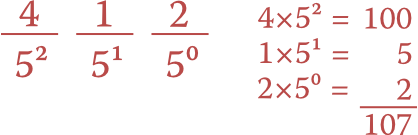
      ‘412’ in base five is 107 in base ten

      Now try the rest yourself.

   2. 42

   3. 2334

   4. 4444

   5. 10000

2. What are the values of the first five columns in base six? Part of it is done for you; complete the rest.

   

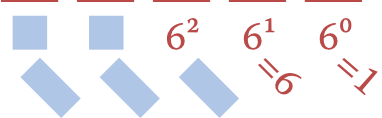
   The columns in base six

3. Convert the following base-seven numbers into base ten.

   1. 42

   2. 616

   3. 500

4. Convert the following base-twelve numbers into base ten, where ‘X’ represents the value ten (dek), and ‘E’ represents the value eleven (ell).

   1. 42

   2. 4X

   3. 100

   4. 2E8

5. Now we’ll try converting in the opposition direction: from base ten to a foreign base.

   1. Convert 651 into base five.

   2. Convert 328 into base nine.

   3. Convert 210 into base six.

   4. Convert 531 into base three.