Auth & Auth

Two of the primary concerns in security are both abbreviated “auth,” but they’re different:

authentication:: This is all about obtaining the accurate identity of a person or a system. In the physical world, we use things like ID cards and facial recognition to authenticate one another.
authorization:: Once we know who you are, authorization is just about what you’re allowed to do, or where you’re allowed to go.

We’ll concentrate mostly on authentication. There are three categories of things that can be used to authenticate you:

Something you know. A password or PIN is a good example. Anyone who knows my email address and password can log in as me on Facebook.
Something you have. A physical, metal key is a good example. Anybody who has the key to my office can open the door and take my stuff.
Something you are (part of your person, aka biometrics.) Humans do this all the time, in the form of facial recognition in person or voice recognition on the phone. The technology for it is still developing, but there are fingerprint scanners, retinal (eye) scanners, and some limited forms of facial and voice recognition.

The best practice is to use two-factor authentication, which means that we require items from two different categories. Here are some examples of two-factor authentication:

When you use an ATM, you present both your bank card (something you have) and your PIN (something you know). Either item alone is not enough to withdraw money.
A photo ID represents two-factor authentication: you have the ID, and the picture on it resembles you (facial recognition). Sometimes the person requesting your ID will also ask your address or birth date, which brings in the third factor (something you know).

Two-factor authentication over the web is a little trickier. Almost all of your web site accounts are based solely on something you know (user name or email address and password). But a few web sites, including Google, try to add other factors. For example, they can ask for your mobile phone number, and then send you a code as a text message. It’s an attempt to bring in something you have (your phone) because most people won’t be able to access their text messages without possessing that device.

Another technique that’s used in some environments is to have a physical device (the RSA SecurID is one such product) that displays a numeric code that changes every 5 or 10 seconds. The codes are unpredictable, but they are synchronized with a device on the server side. To log in, you must provide both a password and the number from the device.

Password hygiene

We can estimate how secure a password scheme is by counting how many possible passwords meet its requirements. For example, a typical four-digit ATM PIN is not very secure at all. It uses only digits, so there are 10 choices (0–9) for each of the 4 positions. That means 10⁴ = 10,000 possible PINs.

The number of possible passwords is proportional to how long it would take, theoretically, to guess the password by “brute force” – that is, trying every possibility. If I found someone’s ATM card, I could stand at an ATM and try entering a different PIN every 2 seconds or so: perhaps starting with 0000 then 0001 all the way to 9999. How long would this take? In the worst case, 10⁴ passwords times 2 seconds each is 20,000 seconds, which is 20,000 ÷ 60 ÷ 60 = 5.5 hours.

Of course, the ATM wouldn’t allow you to try 10,000 different PINs with the same card. After a few errors, it might lock that account and perhaps keep the card. But still, the number 10⁴ (also the 5.5 hours) is a nice way to quantify the theoretical complexity of a PIN.

Let’s apply that calculation to a different password scheme. Suppose we have 6-character passwords made of entirely lower-case letters. Then there are 26 choices for each position, so that’s 26⁶ = 308,915,776. This sounds like a lot, but suppose I write a computer program that tries to log into your account using every possible password. Unlike a human at an ATM, it might be able to try a different password every millisecond. Then the calculation is 308,915,776 ÷ 1000 ÷ 60 ÷ 60 ÷ 24 = 3.6 days. That’s still not very good – if I was determined to get into a wealthy person’s bank account, it’s probably worth writing a small program and waiting four days. (Again, this is a theoretical measure of complexity – computer systems should lock accounts that have too many incorrect login attempts.)

Now we have a way to understand much of the common password advice: that passwords should be long, should use both upper- and lower-case letters, and should use digits and special symbols. We’ll try one more calculation: an 8-character password that can use upper-case, lower-case, and digits. That means each position has the possibility of 26 upper-case + 26 lower-case + 10 digits = 62 choices. Raise that to the 8th power for the number of positions, and we get 62⁸ = 218,340,105,584,896 – a mind-boggling number! Trying one login per millisecond would take up to 218,340,105,584,896 ÷ 1000 ÷ 60 ÷ 60 ÷ 24 ÷ 365 = 6,923 years! This calculation makes it clear that longer passwords with more diverse characters are substantially more secure. (If it takes thousands of years to break into the wealthy man’s bank account, he probably won’t care by then.)

One other piece of advice you may have heard about passwords is that you shouldn’t write them down. Actually, recommendations on this issue are evolving. Many security professionals now think it’s more important never to use the same password for multiple systems. (We’ll see why in the next section.) You probably have dozens (if not hundreds) of accounts on the web, and there’s no way you can remember that many secure, distinct passwords without recording them somehow. Therefore, the best practice is to use a secure password manager. There are several systems that do this, such as LastPass and 1Password.

A secure password manager maintains a database of your login names and passwords, but the database is itself encrypted by a master password, which is the only one you have to remember. Furthermore, the database is only ever decrypted locally, so nobody who has access to their server can see your decrypted passwords. If you forget your master password, all is lost – nobody else will be able to decrypt the database or reset your master password for you.

Password storage

TODO (hashes, dictionary attack)

How to safely store a password by Coda Hale

Cryptography

The word cryptography comes from crypto meaning “hidden” and graph meaning “writing.” The idea is that we want to send messages that can be understood only by the intended recipient. If the message is intercepted by a third party, it will look like nonsense.

Shared-secret systems

These videos offer a good overview of the progression of cryptography over the centuries:

Caesar Cipher & Frequency Analysis (2:36)
Polyalphabetic cipher (2:26)
One-time pad (2:55)

Of these, the one-time pad is the most secure. It is, in fact, considered to be unbreakable, as long as:

The pads are truly and completely random, and
They are never reused.

Below are some graphs I created that show what happens to a frequency analysis as we use each of these encryption methods, in turn. The first one, for comparison, is from a large piece of English text.

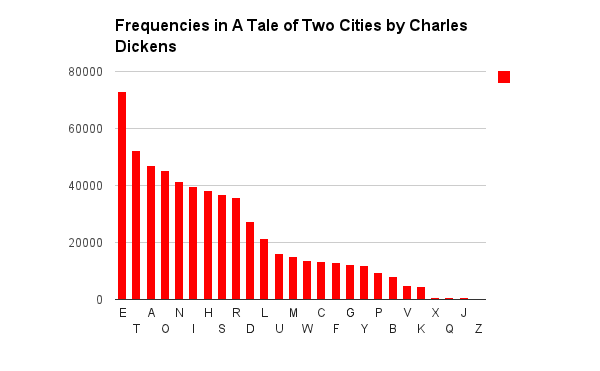
We start by measuring the frequencies of the text of an entire novel.

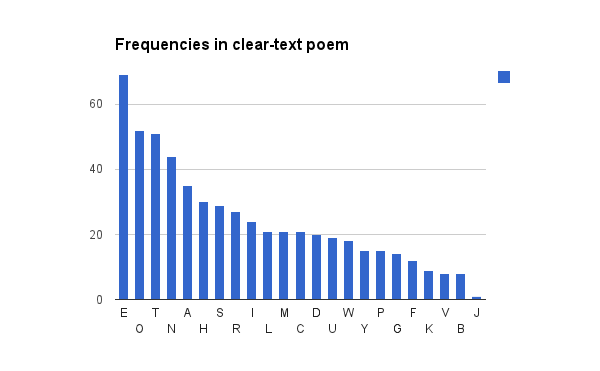
In the (much shorter) clear-text poem, E stands out as most frequent, with other members of ETNORIAS in the top nine. The shape is still very similar.

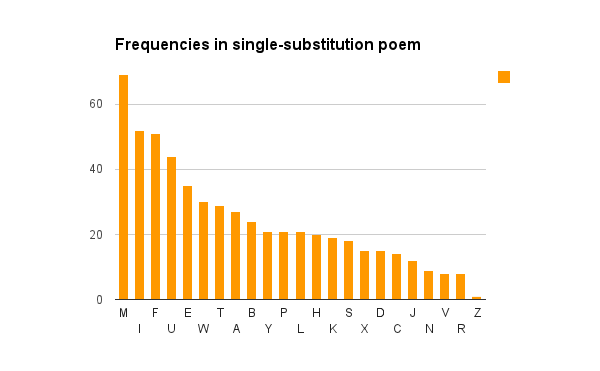
After shuffling the alphabet and doing single-substitution, the frequencies are exactly the same, so it’s a dead giveaway that M→E, F→T, and so on.

Here is my handout about using a poly-alphabetic (Vigenère) cipher.

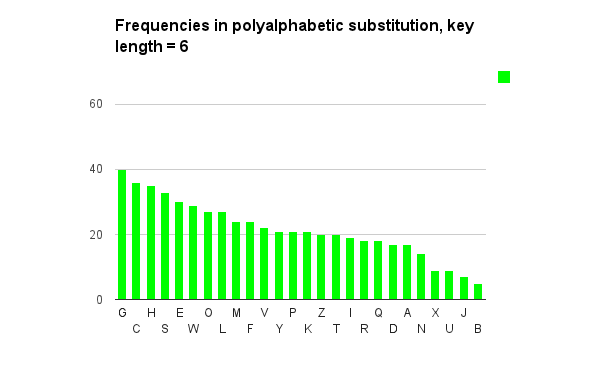
Above we applied a poly-alphabetic cipher, and the frequency differences are less extreme.

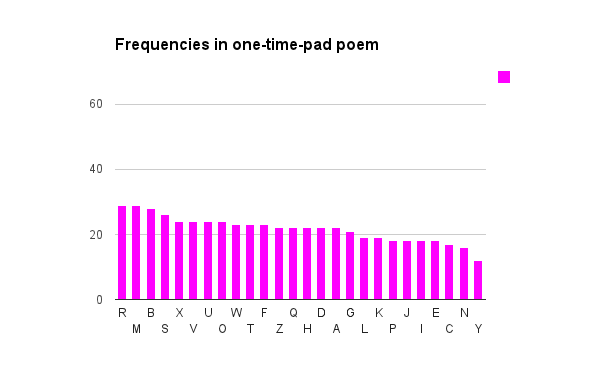
With a random one-time pad, the frequencies are almost uniform. There’s really no correlation between frequent letters here and frequent letters in the clear text.

Here is a fragment of the one-time pad that I generated to encode the poem used for the last graph above.

KGMKJ KGBST NWGNR BBFGA FJUPK DRUIF ZMOPU PMCAS HHWCS LCKMA ZWLVZ FVPFH
YUGKX VJPXF HFEZQ GCMIT CZYGO UYESJ VUVJA UALLK YHEVT GPJZG SHMZI TQTDW

Traditionally, pads are grouped into five characters. Then you write your secret message beneath the pad letters, grouped similarly. Suppose the message is “Attack at dawn”. We’ll regroup that as “attac katda wn” and match it with the pad:

KGMKJ KGBST NWGNR
attac katda wn

Then, you just map the letters to the numbers 0–25 and add using modular arithmetic. So “K+a” is 10+0 = 10 = K. Then “G+t” is 6+19 = 25 = Z. Next, “M+t” is 12+19 = 31 ≡ 5 = F, and so on. The full encoded message is:

KZFKLUGUVTJJ

There’s also a great example and analysis of a Vigenère (polyalphabetic) message from the Civil War, that was finally found and broken in 2011.

Public key systems

One of the serious drawbacks of all the above cryptography techniques is that the sender and receiver must establish a shared secret. That is, they must get together in secret to decide on the alphabet permutation or password, or to create one-time pads. If an eavesdropper is trying to monitor their communications, there’s a good chance that their shared secret will fall into the hands of the eavesdropper too.

The invention of public-key cryptography removes this disadvantage. The key is split into two parts: one that is fully public, and one that is fully private.

Public-key – Diffie-Helman (5:23)
Public-Key – RSA (16:30)

PDF version

Security & Privacy