Assignment 7 – AI
due at 23:59 on +50
In this assignment, you will use a search strategy to solve a puzzle. First, let’s describe the puzzle.
Six frogs are trying to cross a pond by jumping between stones. Alma, Ben, and Carl are heading East; while Xavier, Yolanda, and Zora are heading West. Their initial positions are illustrated in the image.
Each frog can either:
Jump onto an adjacent stone (let’s call this move a slide), or
jump over one other frog, if there is an empty stone on the other side. (A frog can’t jump over more than one frog, and two frogs cannot occupy the same stone.)
Another rule is that the frogs are stubborn, so they refuse to change direction. The A, B, C frogs will only travel East, and X, Y, Z only West.

We’ll be searching for a sequence of moves the frogs can use to cross the pond. The goal state should have Xavier, Yolanda, and Zora (in any order) on the three leftmost stones, and Alma, Ben, and Carl (in any order) on the three rightmost stones.
Here’s a compact way to represent a single state of the frog world. Just use one character for each stone, and a dash or underscore to represent the empty stone. So the start state would be ABC_XYZ, and one potential goal state would be ZYX_ACB.
From the start state, if Carl slides, what state would we be in?
From the start state, if Yolanda jumps (over Xavier), what state would we be in?
From the start state, is it possible for Zora to move? Think about the preconditions that enable different types of moves. (A precondition specifies what must be true to allow the frog to take that action.)
Describe the precondition required for frogs A, B, or C to slide onto an adjacent stone.
Describe the precondition required for frogs A, B, or C to jump over another frog.
Describe the precondition required for frogs X, Y, or Z to slide onto an adjacent stone.
Describe the precondition required for frogs X, Y, or Z to jump over another frog.
The solution to the 6-frog puzzle takes 15 steps! To simplify it for our analysis, let’s exclude two frogs and their two stones. From now on, the start state will just be AB_YZ, and the goal is YZ_AB.
Here is a graph illustrating all states that are within four moves from the start state.
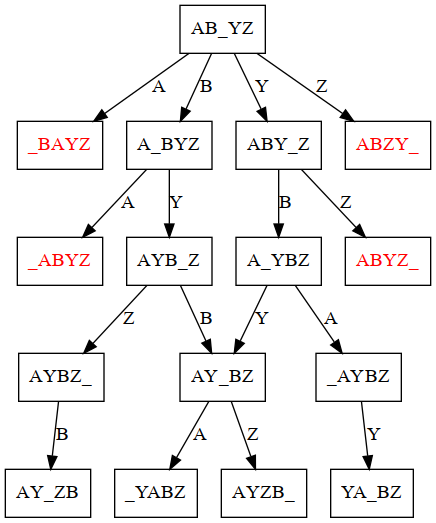
The red nodes are dead ends, because no other move is possible. Each edge is labeled by the frog that moved (whether it is a slide or jump can be determined from the state, and which direction it moves is determined by the frog).
Because frogs only move one direction, the graph for this problem will not have any loops (cycles). It is what we call a directed acyclic graph (DAG).
- Your task is to complete the above graph, showing all possible next-steps from the bottom four nodes. Some will be dead ends, and some will lead to the goal state. Expand the graph and find the solution!
You can submit a combination of text documents and/or image files that include your answers and graphs. The formats doc, docx, txt, pdf, odt, jpg, and png are all fine. Upload the file(s) to this dropbox for assignment 7.