Quiz 3 Solutions
Wed Feb 28
You have up to 20 minutes. You may not use text book or notes.
Write the Boolean expression implemented by the circuit diagram shown in Figure 1.
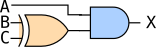
Circuit diagram for question 1 \(A\cdot (B\oplus C)\)
For any Boolean values \(X\) and \(Y\), can \((X+Y)'\) be rewritten as \(X' \cdot Y'\)?
yes / noJustify your answer by creating a truth table to show the results of the two expressions for all possible values of \(X\) and \(Y\).
They are the same. It is illustrated in this truth table, where the values of the two underlined columns are the same.
X Y X+Y (X+Y)' X' Y' X'·Y' 0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 ----- -----In algebra, an operator is commutative if the order of its operands can be switched. For example, standard addition is commutative because \((A+B) = (B+A)\) for all numbers \(A\) and \(B\). Division is not commutative. For example, \((4\div5) \neq (5\div4)\) or in decimal notation, \(0.8 \neq 1.25\).
Which of the Boolean operators (AND, OR, XOR) are commutative? (Choose none, one, two, or all of them.)
All of those operators are commutative. You can tell by looking at the middle two rows of a truth table – the ones were \(A\neq B\). The results are the same regardless in which order \(A\) and \(B\) appear.