These are rough notes from our meeting on Thursday 19 January.

We (I) decided to pursue a project in deep reinforcement learning, perhaps with application to game-playing. I referenced these projects and papers:

OpenAI Universe
Metalforge Crossfire
Human-level control through deep reinforcement learning, Nature 518, 26 February 2015

Basics

To begin exploring this area, we started with the simplest artificial neural networks, known as perceptrons. This formulation began with McCulloch and Pitts in 1943! (I was off by a few decades in class.)

We have a graph in which both nodes (circles) and edges (lines) are assigned real numbers in some range, typically 0..1 or -1..+1, but other ranges can be used too. Numbers assigned to nodes are called activation levels, and numbers assigned to edges are called weights.

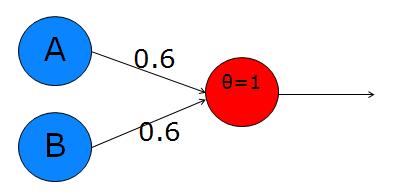
Sample Perceptron from this overview

In this perceptron, let’s call the two input nodes (left layer) A and B, and the output node is C. The upper edge weight will be \(w_a\) and the lower edge weight is \(w_b\). The main calculation is just a weighted average: \(C = A·w_a + B·w_b\).

But then we also apply a function to the result, to adjust its range and kind of “snap” it into a positive or negative result (activated or inactive). This function can be a simple “step” with a given threshold \(t\), such as \(t=0.5\) or \(t=1.0\):

\[ f(x) = \biggl\{\begin{array}{ll} 0 & \mbox{if}\; x < t\\ 1 & \mbox{if}\; x \ge t\\ \end{array} \]

Step function, with threshold \(t=0\). [Source]

Later on, we may use a more sophisticated function that smooths out the discontinuity at the threshold, like this one, called the Sigmoid function:

\[ f(x) = \frac{1}{1+e^{-x}} \]

The “logistic” sigmoid (formula above), centered on \(x=0\). [Wikimedia]

It’s interesting to see if we can make perceptrons emulate the Boolean logic operators, like AND, OR, NOT, XOR. The perceptron above, with weights \(w_a=0.6\) and \(w_b=0.6\) implements OR:

A B  C = f(A*Wa + B*Wb)
0 0  f(0*0.6 + 0*0.6) = f(0)   = 0
0 1  f(0*0.6 + 1*0.6) = f(0.6) = 1  (because 0.6 > t)
1 0  f(1*0.6 + 0*0.6) = f(0.6) = 1
1 1  f(1*0.6 + 1*0.6) = f(1.2) = 1

Here we’re using the step function with threshold \(t=0.5\).

We can implement Boolean AND with \(w_a=0.4\) and \(w_b=0.4\):

A B  C = f(A*Wa + B*Wb)
0 0  f(0*0.4 + 0*0.4) = f(0)   = 0
0 1  f(0*0.4 + 1*0.4) = f(0.4) = 0  (because 0.4 < t)
1 0  f(1*0.4 + 0*0.4) = f(0.4) = 0
1 1  f(1*0.4 + 1*0.4) = f(0.8) = 1  (because 0.8 > t)

XOR

A problem arises with the XOR function. Minsky and Papert showed that this simple perceptron model cannot encode XOR. (And their influence set back research into artificial neural networks for a decade or more!) A perceptron can model (and learn) any function that is linearly separable, but XOR is not.

The trick to making this model more powerful is to add a “hidden” layer between the input nodes and the output node. Then you fully-connect the nodes of the input layer with those in the hidden layer. That produces a graph with five nodes and six edges:

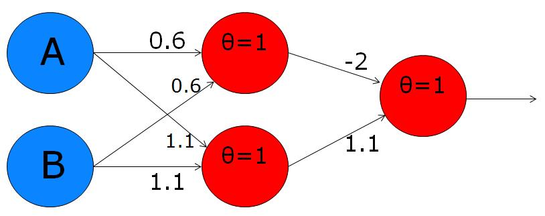
XOR implementation with hidden layer

We struggled a bit with getting this to work, but Priya figured it out! The solution is to set the threshold of the step function to 1. Below is her work:

Full resolution

In retrospect, I now understand the use of the θ (theta) label in these diagrams: it indicates the threshold value to use to assign a value to the labeled node. So \(θ=1\) was staring us in the face!

Code

Below is a sketch of a small C++ program to implement simple fixed-size perceptrons (three nodes, two edges). It includes a main program that – once the functions are working correctly – will print the truth tables for AND, OR, and NAND! See the sections marked “TODO”. Here is the expected output:

AND:
0 0: 0
0 1: 0
1 0: 0
1 1: 1
OR:
0 0: 0
0 1: 1
1 0: 1
1 1: 1
NAND:
0 0: 1
0 1: 1
1 0: 1
1 1: 0

// Simple perceptron logic gate implementation
#include <iostream>
using namespace std;

float step_function(float threshold, float value)
{
  // TODO
  return 0;
}

float run_perceptron(float weightA, float weightB,
                     float valueA, float valueB,
                     float threshold)
{
  // TODO
  return 0;
}

void show_truth_table(float weightA, float weightB,
                      float threshold)
{
  // TODO: call run_perceptron 4 times,
  // feeding it all four values of A,B.
}

int main()
{
  cout << "AND:\n";
  show_truth_table(0.4, 0.4, 0.5);
  cout << "OR:\n";
  show_truth_table(0.6, 0.6, 0.5);

  // TODO: can you figure out two weights and a threshold
  // that will implement "NAND"? This is the opposite of AND.
  cout << "NAND:\n";
  show_truth_table(0,0,0);
  return 0;
}

PDF

Perceptrons

Basics

XOR

Code