Assignment 2
Due Monday 1 October in class.
Write your first name in binary and hexadecimal, using the ASCII encoding. Here is mine, as an example:
C h r i s (text) 67 104 114 105 115 (decimal) 01000011 01101000 01110010 01101001 01110011 (binary) 43 68 72 69 73 (hex)Decode the following message. Each chunk is an 8-bit binary number representing the ASCII code for a letter.
01010011 01110100 01110101 01100100 01011001 00100001Use truth tables to prove the equivalence of these two Boolean expressions:
X·Y + X'·Z + Y·Z = X·Y + X'·ZBelow is a reasonably complex combinational circuit diagram. It contains three XOR gates, three AND gates, and one OR gate. It has four inputs (labeled A, B, C, D – the strange order is intentional), three outputs (labeled X, T, S), and four intermediate wires (labeled E, F, G, H). Make sure you can find all those components before moving on.
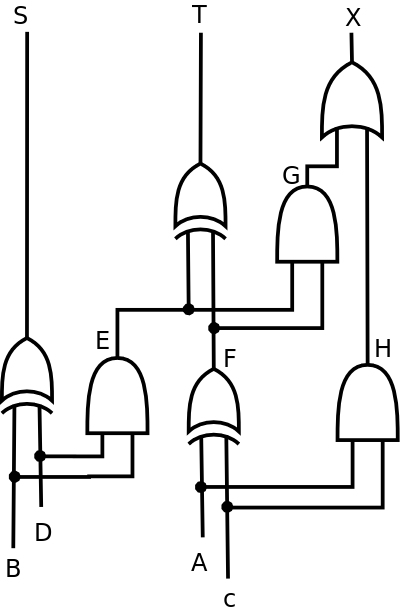
Adder
Your task is to determine how this circuit will react to various inputs, by filling in the truth table below.
A B C D E F G H X T S 0 0 0 0 _ _ _ _ _ _ _ 0 0 0 1 _ _ _ _ _ _ _ 0 0 1 0 _ _ _ _ _ _ _ 0 0 1 1 _ _ _ _ _ _ _ 0 1 0 0 _ _ _ _ _ _ _ 0 1 0 1 _ _ _ _ _ _ _ 0 1 1 0 _ _ _ _ _ _ _ 0 1 1 1 _ _ _ _ _ _ _ 1 0 0 0 _ _ _ _ _ _ _ 1 0 0 1 _ _ _ _ _ _ _ 1 0 1 0 _ _ _ _ _ _ _ 1 0 1 1 _ _ _ _ _ _ _ 1 1 0 0 _ _ _ _ _ _ _ 1 1 0 1 _ _ _ _ _ _ _ 1 1 1 0 _ _ _ _ _ _ _ 1 1 1 1 _ _ _ _ _ _ _ Each cell in the table should be relatively straightforward to compute, you just have to approach them very systematically. For example, we see from the diagram that E = B·D (the Boolean AND gate). So looking at the values of B and D in each row, you compute 0·1=0, then 1·1=1, etc. For the XOR gates, remember that they only produce 1 if there is exactly one input that is on.
To check your work, it helps to know that this diagram has an important meaning. It is a half-adder combined with a full-adder, able to compute the sum of any two-bit binary numbers.
For each row, interpret AB as a two-bit number, and CD as another. The sum of them should be the value of the three-bit number XTS. That is, for the row “1011”, AB = 10₂ = 2₁₀ and CD = 11₂ = 3₁₀. Add these numbers to get 5₁₀ = 101₂. Thus, your outputs should be 101.
Continue that reasoning for each row and make sure there are no mistakes. I will evaluate your output bits, intermediate steps, as well as the work you do to check your results.