Quiz 1 Solutions

[4 points for showing up]

Using 7-bit signed (two’s complement) binary numbers, what is the largest positive number? What is the smallest negative number? [6 points]

In 7-bit two’s complement, the column values are:
```
  ___  ___  ___  ___  ___  ___  ___
  -64  32   16    8    4    2    1
```
So the largest positive number is 0111111 = 63 and the most negative number is 1000000 = -64.

Convert the following 16-bit binary number into hexadecimal. [6 points]

8 4 2 1  8 4 2 1  8 4 2 1  8 4 2 1
-------  -------  -------  -------
0 1 1 1  1 1 1 1  0 0 1 1  1 0 1 0

    7       F       3       A

Add and verify the following unsigned binary numbers. [6 points]

  1 1 1 1 1                      1     1
  1 0 1 1 1 1  = 47                1 1 0 1 1 1  = 55
+ 0 1 1 1 0 1  = 29              + 1 0 0 1 0 0  = 36
--------------   --              --------------   --
1 0 0 1 1 0 0  = 76              1 0 1 1 0 1 1  = 91

  32  8   2                        32  8   2  
64  16  4   1                    64  16  4   1

Suppose we need to send a text message uses just 15 distinct characters. How many bits per character are required if we’re using a fixed encoding? [6 points]

We need 4 bits per character, which allows 16 distinct characters to be represented.
Draw a binary tree that corresponds to the following variable-width encoding of four characters. The characters should appear in boxes at the leaves. Branch left on a zero, or right on a one. [6 points]
```
T 00  
R 010 
N 011 
O 1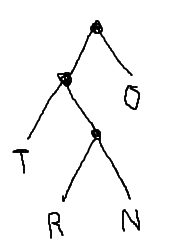   
```
Use the character encoding from the previous question to decode the following word: [6 points]
```
0 0,1,0 1 0,1,0 1 1,0 0,1
  T O     R O     N   T O
```