(Other) Programming languages
The variety of languages
There are many different programming languages available. The language sometimes targets particular platforms (such as Objective-C for Mac and iOS development) particular types of applications (such as C/C++ for system and driver development) or particular ideas about how to structure computations (such as Haskell for typed functional programming).
Here is one snapshot of language popularity at a point in time, but we must take it with a grain of salt. These results are highly dependent on the technique used to measure popularity, so different studies can yield very different results.
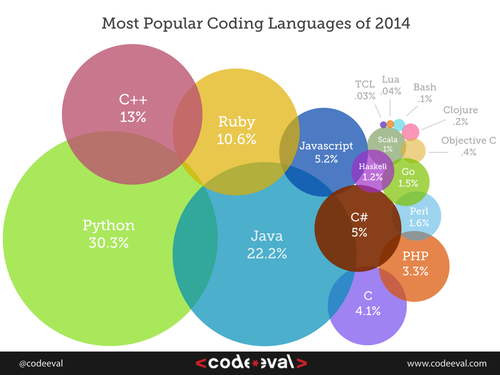
The popularity of languages waxes and wanes over the decades. A professional software developer is not likely to use the same language across her entire career. One organization that famously measures language trends is TIOBE (and you can see that they don’t rate Python nearly as highly as the figure above).
Language taxonomy
Languages can be grouped by their features in various ways. One of the highest-level groupings in the language family tree is imperative vs. declarative languages. Imperative languages work primarily by issuing a sequence of commands. (One dictionary definition of ‘imperative’ is “giving an authoritative command.”) In our work on Python, each statement we type is a new command, telling the computer to do things such as print some text, do some calculation, or update a variable. In declarative languages, programs characterize their computational goals without explicitly stating what steps must be performed. This is a little hard to imagine (and most declarative languages include some imperative elements too), but the examples below in Prolog help to make it more concrete.

The imperative family is further divided into procedural and object-oriented languages. In a procedural language, the program is sub-divided into procedures, which are themselves sequences of steps to solve a particular problem. Procedures are also called subprograms or functions. In an object-oriented language, the main organizational principles is objects (or classes of objects), which are modules with both procedures and data structures encapsulated within them. The various objects in a program solve problems by sending messages and responding to each others’ messages, much like human organizations work.
As a beginning programmer, most languages you’ve heard of are imperative, and are a combination of procedural and object-oriented. This includes Python, Java, and C++. A language like C (the older subset of C++) is mostly procedural, with very little support for objects. And some other languages, like Smalltalk and Ruby, are perhaps more object-oriented than procedural. But these boundaries are rather blurry.
Here is a Python example of an imperative approach to calculating the factorial of a number. Notice how each statement contains a command: set a variable, repeat this, section, set more variables, return a result.
def fact(n): # Factorial function, imperative style, Python
k = 1
while n > 1:
k = k * n
n = n - 1
return kWithin the declarative camp, other subdivisions are functional, logic, and query languages. Functional languages work primarily using mathematics-style functions. This means that each piece of code throughout a program produces a value, and can be replaced with its value without any side effects. The math function sin(x) produces a value, and always the same value for any particular x. Examples of functional languages include Haskell and Scheme (a dialect of Lisp, which is one of the oldest languages).
Logic languages are based on predicate logic, which is a branch of mathematics that deals with formal reasoning about and/or (the Boolean operators), but also implication, relations, and inference. The primary example of a logic language is Prolog.
Finally, query languages are a declarative way to characterize some subset of data in a database. The primary example is SQL (which we’ll learn later), but there are a few others in less common use.
Here is a more declarative approach to calculating the factorial of a number. It’s written in the functional language Haskell, and just says that the factorial of N is the product of all the integers from 1 to N.
fact n = product [1..n] -- Factorial, functional style, HaskellExpression notation
A very concrete way in which some languages differ is how arithmetic expressions are written. The normal way we write expressions, such as \(a+b\) is called “infix” because the operator (\(+\)) is in between the operands (\(a\) and \(b\)). But there are alternatives, called prefix and postfix. Collectively, they are also called “Polish notation” (forward Polish for prefix, or reverse polish (RPN) for postfix).
The Lisp language family (which includes Scheme, Racket, Clojure, and others) use prefix notation. They also surround each sub-expression with parentheses, so here is the way to write \(1+2\times3\):
(+ 1 (* 2 3))You evaluate prefix expressions starting from the innermost parentheses, like this:
(+ 1 (* 2 3)) ⇒
(+ 1 6) ⇒
7A few language use postfix notation. No parentheses are needed at all, you just specify the numbers (separated by spaces) and the operators. So that same calculation, \(1+2\times3\), looks like this:
1 2 3 * +When converting an infix expression to prefix or postfix, it’s helpful to draw a tree representing the expression. You do this by joining the operands of each operator, in the order you would apply them (according to the standard order of operations). Here is a tree for the expression \(180-6\times(2+7)\times3\):
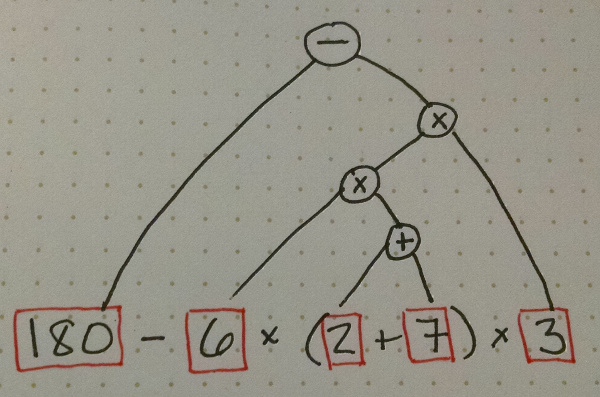
To convert it to prefix, each node (starting from the root) corresponds to a set of parentheses, and then you convert the left node and the right node after writing the operator:
(- 180 (* (* 6 (+ 2 7)) 3))To convert to prefix, you start from the root, but for each node you complete the left and right sub-trees before writing the operator in that node:
180 6 2 7 + * 3 * -Postfix is also quite easy to calculate, which is why it was a popular choice in the early days of computing for simple devices with little memory, like calculators and printers. To calculate directly in postfix, you use a stack. Each time you see a number, you push it onto the stack. Then when you see an operator, you remove the top two elements of the stack, apply the operator, and push the result. Here is an illustrated example, in which we calculate the result of this expression.
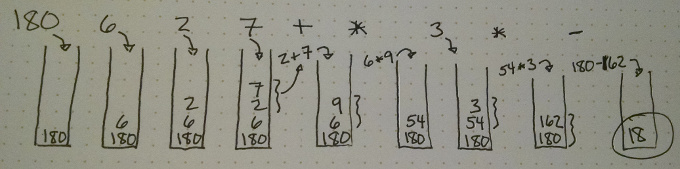
And finally here it is being evaluated in two programming languages: Scheme (Racket) and Postscript (Ghostscript).
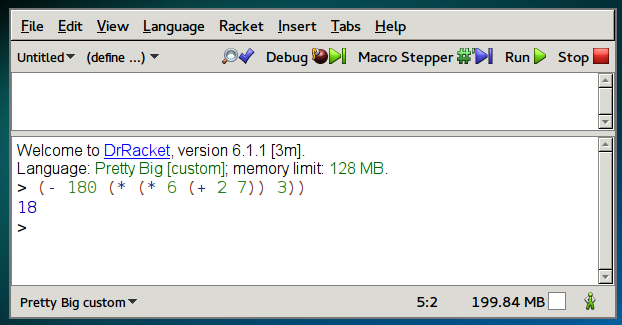
Postscript is a language used primarily by printers, but pieces of it are also integrated into PDF, which is a document format you probably use pretty often. In Postscript, the operators are spelled out as words, like add and mul. The operator pstack prints the contents of the stack, and then pop removes the top element of the stack.
GPL Ghostscript 9.15 (2014-09-22)
Copyright (C) 2014 Artifex Software, Inc. All rights reserved.
This software comes with NO WARRANTY: see the file PUBLIC for details.
GS> 180 6 2 7 add mul 3 mul sub pstack pop
18Here are some videos that further explain the differences between infix, prefix, and postfix.
Infix, prefix, postfix (mycodeschool, 13 min)
Postfix and stacks (Computerphile, 13 min)
RPN on trees (Computerphile, 10 min)
Prolog example
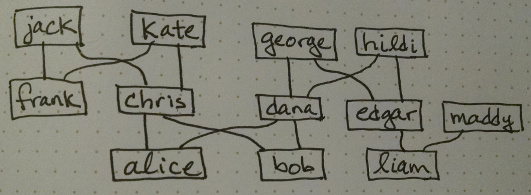
% family.prolog -- representing and deducing a family tree
% First we specify the parent-child relationships.
% parent(A,B) is read as "A is a parent of B."
parent(chris, alice).
parent(chris, bob).
parent(dana, alice).
parent(dana, bob).
parent(edgar, liam).
parent(george, dana).
parent(george, edgar).
parent(hildi, dana).
parent(hildi, edgar).
parent(jack, chris).
parent(jack, frank).
parent(kate, chris).
parent(kate, frank).
parent(maddy, liam).
% Next we can define other relations in terms of parent.
% Capital letters can be replaced by any matching person.
grandparent(X,Y) :- parent(X,Z), parent(Z,Y).
% Sample queries:
% List all the grandparents of alice:
% ?- grandparent(X, alice).
% X = george ;
% X = hildi ;
% X = jack ;
% X = kate .
% List all the grandchildren of hildi:
% ?- grandparent(hildi, X).
% X = alice ;
% X = bob ;
% X = liam .
% We can define relations recursively. Your parent is your ancestor, and
% any ancestors of your parents are also your ancestors.
ancestor(X,Y) :- parent(X,Y).
ancestor(X,Y) :- parent(Z,Y), ancestor(X,Z).
% Sample queries:
% List all ancestors of bob:
% ?- ancestor(X, bob).
% X = chris ;
% X = dana ;
% X = jack ;
% X = kate ;
% X = george ;
% X = hildi .
% Siblings have two (different) parents in common.
sibling(X,Y) :- parent(P1,X), parent(P1,Y),
parent(P2,X), parent(P2,Y),
dif(P1,P2), dif(X,Y), P1 @< P2.
% Sample queries:
% ?- sibling(X, alice).
% X = bob .
%
% ?- sibling(frank, X).
% X = chris .
% An aunt or uncle is a sibling of my parent.
uncle(X,Y) :- parent(Z,Y), sibling(X,Z).
% Sample queries:
% ?- uncle(X, alice).
% X = frank ;
% X = edgar .Further reading
- Seven things you should know if you’re starting out programming by Jonathan Richards in The Guardian.