Assignment 1 – text compression
due at 23:59 on +50
Introduction
In this activity, we will investigate the Huffman algorithm for text compression. You’ve already seen one example of a Huffman encoding, represented by the strange-looking tree on the handout labeled “variable-bit Huffman encoding.”
You will follow the Huffman algorithm and create a tree of your own, based on the character frequencies of a message that I provide. The video below illustrates the algorithm on paper. I apologize that the resolution and audio quality aren’t great, but it should be understandable. The final encoding and tree are also pictured below.
*Error at 21:54 – 39×5 should be 195 bits.
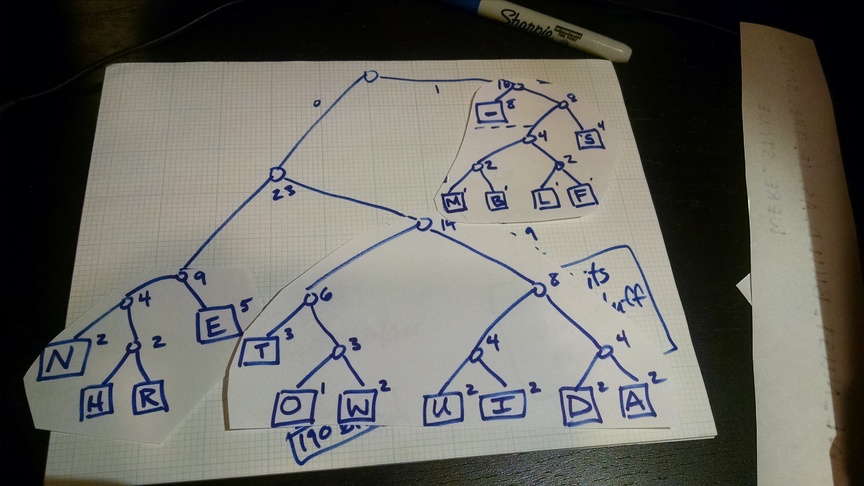
The tree I produced

Encoding the phrase using that tree, result is 148 bits
You should also answer the following questions.
How many distinct characters did your message contain?
If we were using a fixed-width encoding, how many bits (per character) would you need to represent just those characters?
What is the most frequent character in your message, and how many times did it appear?
How many bits are used to represent the most frequent character in your message?
What is the most number of bits used to encode any character in your message?
Use the tree you produced to encode the entire message you were given. How many bits are used, in total?
The technique in the rest of this document refers to using sticky notes and only drawing the tree at the end. Either way, the result should be the same. (The sticky notes were a little harder to manage on video.) If you were able to get your tree and answer the six questions above then you’re done – submit as follows.
How to submit
Take a photo of the tree you drew that represents your variable-width Huffman encoding. Try to make it as legible as possible – redraw on a fresh sheet of paper if needed.
Write your answers to the six questions into a text document – the formats .doc, .docx, .txt, or odt are all fine.
Upload both files to this dropbox for assignment 1
Phase 1: count letter frequency
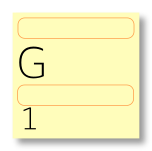
Start with a stack of blank sticky notes and the message you were given. We’re going to consider each of the characters in your message, in order. Suppose the first character is a G. We would write the G on a sticky note – roughly at the center left – and also begin a tally in the lower left corner. Leave some space above and below the character, as shown:
Move on to the next character in your message. Assuming it is a different character, make a new sticky for that one.
When you encounter a character that you’ve seen before, do not create a new note, but instead update the tally on the existing note containing that character. In this example, we’ve just seen the character E for the third time:
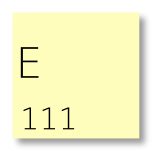
Continue doing this for the entire length of your message. You will now have a count of the frequencies of each character. Write the frequency in conventional (base ten) notation in the upper left. Here’s a small sample:
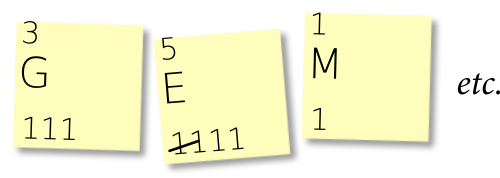
In the next section, we will process these characters in order from lowest frequency to highest. So you may want to take a moment now to arrange them in roughly that order on your desktop.
Phase 2: merge tiles
The algorithm continues by repeatedly merging sticky notes, as described here. Start by choosing two notes with the lowest frequencies. Probably you had several characters with a frequency of one, so you can just choose two of them arbitrarily. Place them side by side in your work area:
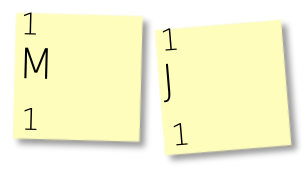
In the section beneath the character and starting from the right, write a zero on the left note and a one on the right note:
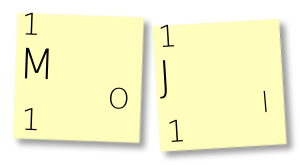
Then, stick the right one onto the bottom of the left one. Cross out the frequencies and replace the top one with their sum – in this case, 1+1 is 2:
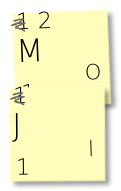
Now you will treat this ‘merged’ note as if it were a single one, so place it somewhere among other characters with frequency=2.
Continue merging together your lowest-frequency letters like this. It’s okay to pair a frequency=1 with a frequency=2 if it’s the last frequency=1 remaining – then the merged frequency would be 3.
Before long, you’ll have to merge notes that themselves are already merged. In the example below, we paired the last frequency=1 character (K) with a group (MJ) that has frequency=2:
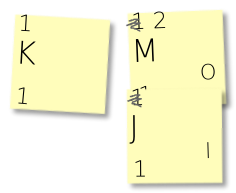
As before, we write a zero on the left note. And we write ones on all of the right notes… to the left of whatever code is already there:
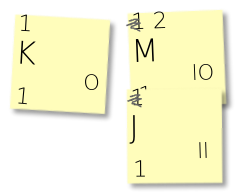
Again, stick the right note onto the bottom of the left one. Cross out the frequencies and replace the top one with their sum – in this case, 1+2 is 3.
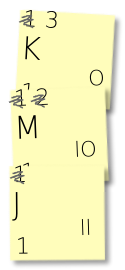
Continue merging notes using this technique until every character in your message is merged into one big note. Then you will have a distinct binary encoding underneath each character. Probably you should take a photo of your encoding, and/or write down the bits produced for each character elsewhere.
Visualize encoding as a tree
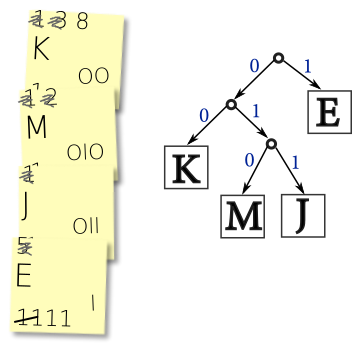
As in the handout on variable-bit Huffman encoding, the character encodings you produced should fit nicely into a binary tree. I’ll do a small example below. Our algorithm has produced the encodings 00 for K, 010 for M, 011 for J, and 1 for E.
We interpret a 0 as choosing the left path in a binary tree, and 1 as the right path. So to get to the K from the root we would go left, twice. For the E, we go right just once. The M and J both have the prefix 01, so they sit at a “sub-tree” reached by going left then right.