Boolean logic
1 Boolean algebra and logic gates
In the 1840s, English mathematician George Boole developed an algebra (a set of operators and laws) for variables that can have just two states – true and false. Thus, a Boolean value is equivalent to one bit:
| False | 0 | off |
| True | 1 | on |
The operators defined by Boole are pervasive throughout all of computing. You may have encountered them in doing library or other database searches. The ones we’ll consider are:
The figure illustrates both the algebraic notation and the circuit
diagram notation. The elements of circuit diagrams are called
gates, as in “AND gate” or “XOR gate.” The “XOR” (⊕) operator is
named for “exclusive OR.”
The behavior of these operators can be defined by truth tables:
A |
B |
A·B |
A+B |
A' |
A⊕B |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
The first two columns indicate the values of the two variables, A
and B. There are four rows because two variables can take on four
different values (22 = 4). If there were three variables, there would
need to be 23 = 8 rows.
2 Combinational circuits
We combine the gates into combinational circuits to achieve various
effects. For example, the algebraic expression X = A·B + A·C
corresponds precisely to the following circuit diagram:
and we can discover its results by completing the truth table:
A |
B |
C |
D=A·B |
E=A·C |
X=D+E |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Exercise: Try drawing the circuits and the truth tables for X=(A·B)'
and for Y=A'+B'. They should produce the same result for all inputs
A and B. This is one of DeMorgan’s Laws.
Show answers
3 Sequential circuits
We’ll just look at the S-R (NAND) latch.
This is a sequential circuit, rather than combinational. That means it contains cycles. One way to make sense of a cycle is to think in terms of the values of wires from one moment to the next. You can subscript each variable with the time of interest: St vs St+1, etc.
M[t+1] = (S · N[t])' N[t+1] = (M[t] · R)'
S |
R |
M[t] |
N[t] |
M[t+1] |
N[t+1] |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
- Video: Flip Flops, Latches, & Memory from Computerphile [8m 53s]
4 Logisim software
This section refers to a program called Logisim, which should run on any platform with a Java Runtime Environment.
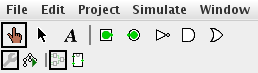
Once you open Logisim, there are a few tools you should familiarize yourself with. The hand tool (leftmost on the toolbar) allows you to turn inputs on and off. The arrow tool (next to it) allows you to place components onto the grid, move them around, and wire them together.
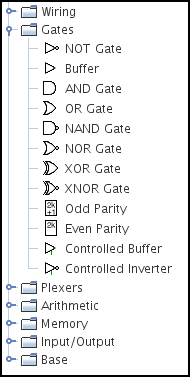
In the side-bar, the main components we’ll be using are in the Gates section, but there’s also the Pin (under Wiring) and the LED (under Input/Output).
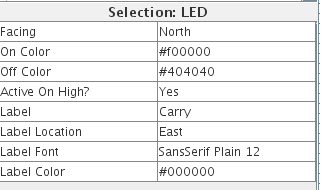
When you have a component selected, its properties appear in the lower left of the screen. You can use these to create a label for your pins and LEDs.
Here is the 3-bit adder circuit I did in class. If that file doesn’t open automatically in Logisim, you can start Logisim first and then use File » Open.
- Video: Logisim tutorial from ENGRTUTOR [7m 47s]
5 Further exploration
- Video: Building a half-adder using dominoes, with Matt Parker on Numberphile [18m 30s]
- Video: The big domino adder, demonstrated at the Manchester Science Festival, UK [22m 26s]
@Cmdr_Hadfield on Twitter