Other programming languages
Arithmetic notation
One very concrete way in which some languages differ is how arithmetic expressions are written. The normal way we write expressions, such as \(a+b\) is called “infix” because the operator (\(+\)) is in between the operands (\(a\) and \(b\)). But there are alternatives, called prefix and postfix. Collectively, they are also called “Polish notation” (forward Polish for prefix, or reverse polish (RPN) for postfix).
Prefix expressions
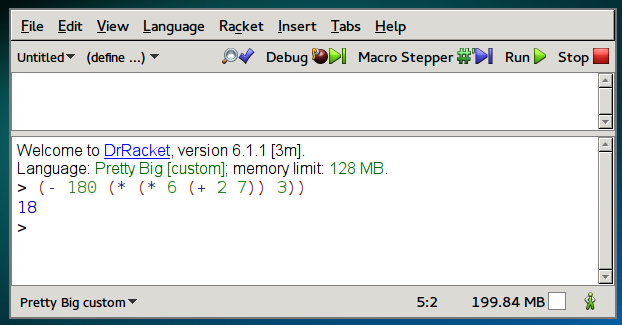
The LISP language family (which includes Scheme, Racket, Clojure, and others) use prefix notation, so the operator comes before the operands. They also surround every sub-expression with parentheses, as in this example:
(/ 36 (* (+ 1 5) 4))
You evaluate prefix expressions starting from the innermost parentheses, like this:
One interesting advantage of prefix is that operators can have any number of operands:
(+ 3 7 10) → 20
Postfix expressions
A few languages use postfix notation. No parentheses are needed at all, you just specify the numbers (separated by spaces) and the operators. So the same calculation performed in the previous section would look like this:
36 1 5 + 4 * /
To evaluate this, you just work from left to right. When you encounter an operator, grab the two previous items to use as operands. Replace all three with the resulting value.
Postfix evaluation is computationally very simple – it is especially suitable for devices with severe memory constraints. It was popular for 1970s calculators, and printers even today. The core of the Portable Document Format (PDF) is a language called Postscript, which is based entirely around postfix evaluation.
Converting between notations
When converting an infix expression to prefix or postfix, it’s helpful to draw a tree representing the expression. You do this by joining the operands of each operator, in the order you would apply them (according to the standard order of operations). Here is a tree for the expression \(180-6\times(2+7)\times3\):
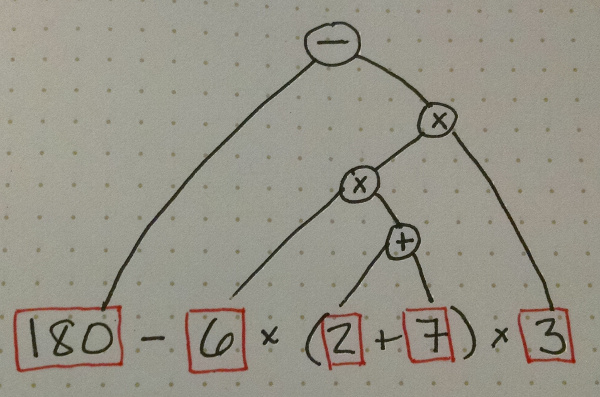
To convert it to prefix, each node (starting from the root) corresponds to a set of parentheses, and then you convert the left node and the right node after writing the operator:
(- 180 (* (* 6 (+ 2 7)) 3))
To convert to prefix, you start from the root, but for each node you complete the left and right sub-trees before writing the operator in that node:
180 6 2 7 + * 3 * -
Here are some videos that further explain the differences between infix, prefix, and postfix.
- Infix, prefix, postfix (mycodeschool, 13 min)
- Postfix and stacks (Computerphile, 13 min)
- RPN on trees (Computerphile, 10 min)