More algorithms
Arrays
An array is a sequence of variables with the same name, and distinguished by an integer index. We use the notation A[3] to provide both the name of the array (A) and the index (3). That operation is pronounced “A at 3” or “A sub 3.” The index usually starts at zero, so in an array with six elements they are numbered zero through five.
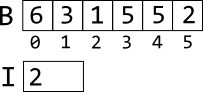
Referring to the array and variable above, we can use the following expressions.
B[1]⇒3B[I]⇒B[2]⇒1B[I+3]⇒B[2+3]⇒B[5]⇒2B[I]+3⇒B[2]+3⇒1+3⇒4B[B[I]]⇒B[B[2]]⇒B[1]⇒3
Selection sort
1. Let A be an array of N integers
2. For each I in the range 0 … N-2,
repeat steps 3 to 6:
3. Set M to I
4. For each J in the range I+1 … N-1,
repeat step 5:
5. If A[J] < A[M] then set M to J
6. Swap A[I] with A[M]The “for each” instructions mean we set the variable to the first value in the range, do the indicated steps, and then set the variable to the next value in the range and repeat.
You can trace this algorithm for any given A and N. Try these:

Fibonacci
We looked a little bit into the Fibonacci sequence, because it was produced by one of the algorithms on quiz 3. Here is a great video series on Fibonacci numbers and plants, by Vi Hart. She has tons of other great videos that explore the beauty and wonder of mathematics. Enjoy!