module A05Sol where
import Data.Maybe (isJust)

Here is an implementation of a tree that stores values only at the interior branches; the leaves are empty.

data ITree a
  = ILeaf
  | IBranch a (ITree a) (ITree a)
  deriving (Show, Eq)

Here is a link to lots of sample trees, with diagrams, built using these constructors.

Functor instance

You should instantiate the Functor type class for ITree, so we can do this:

ghci> fmap square t1
IBranch 9 (IBranch 16 ILeaf (IBranch 25 (IBranch 49 ILeaf ILeaf) ILeaf))
          (IBranch 81 ILeaf ILeaf)
ghci> fmap show t1
IBranch "3" (IBranch "4" ILeaf (IBranch "5" (IBranch "7" ILeaf ILeaf) ILeaf))
            (IBranch "9" ILeaf ILeaf)

That means using the instance keyword and defining the function fmap for the ITree type. There are two examples of Functor instantiations in the notes from 8 Oct.

instance Functor ITree where
  fmap _ ILeaf = ILeaf
  fmap f (IBranch v l r) = IBranch (f v) (fmap f l) (fmap f r)

Mirroring a tree

Define the function flipTree that swaps the left and right branches throughout the entire tree.

flipTree :: ITree a -> ITree a

flipTree ILeaf = ILeaf
flipTree (IBranch v l r) = IBranch v (flipTree r) (flipTree l)

Below is a figure of a tree and its flipped counterpart:

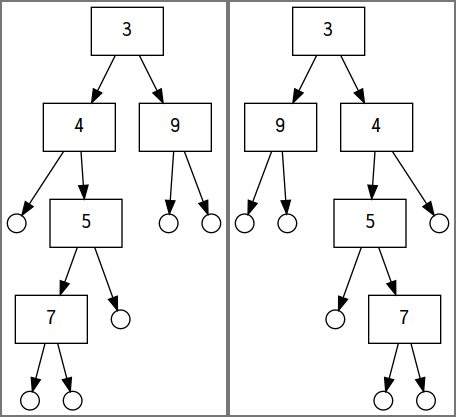
The tree t1 (left) and the result of flipTree t1 (right) — The tree `t1` (left) and the result of `flipTree t1` (right)

Converting to list

This function converts a tree to a list.

preOrderList :: ITree a -> [a]

preOrderList ILeaf = []
preOrderList (IBranch x l r) =
  x : preOrderList l ++ preOrderList r

The elements of the list should be ordered according to a pre-order traversal. That means for a branch, the element at that branch comes first, then the elements of the left sub-tree, then the right sub-tree.

So the pre-order traversal of t1 is:

ghci> preOrderList t1
[3,4,5,7,9]
ghci> preOrderList $ flipTree t1
[3,9,4,5,7]

Is tree balanced?

A tree is balanced if at every branch, the difference in height between the left and right sub-trees is at most one. We’re going to determine whether a tree is balanced by returning a Maybe Int. If the result is Nothing then the tree is not balanced. A Just result indicates it is balanced, with the specified height.

balancedHeight :: ITree a -> Maybe Int

ghci> balancedHeight t1
Nothing
ghci> balancedHeight t7
Just 4

(You can see pictures of these sample trees, t1 and t7, on this page.)

balancedHeight ILeaf = Just 0
balancedHeight (IBranch _ t1 t2) =
  case balancedHeight t1 of
    Nothing -> Nothing
    Just n1 ->
      case balancedHeight t2 of
        Nothing -> Nothing
        Just n2 ->
          if abs (n1 - n2) > 1 then Nothing
          else Just (1 + max n1 n2)

The way to approach balancedHeight for a branch is to recursively compute the height of the left and right sub-trees. If either of those produces Nothing, then we also return Nothing. If those produce Just n1 for the left and Just n2 for the right, then we check the absolute value of the difference. If that difference is larger than 1, return Nothing. Otherwise use Just with the usual height formula: one more than the maximum height of left and right!

If we just want a Boolean to indicate balanced or not, we can compose with isJust from the Data.Maybe module:

isBalanced :: ITree a -> Bool
isBalanced = isJust . balancedHeight

Building balanced trees

Finally, we’d like to be able to take a list of elements and build a balanced tree. That means splitting the list in half (you can use take and drop).

balancedFromList :: [a] -> ITree a

Make sure that the list corresponds to a preorder traversal of the tree. That is, for any tree t, we should have:

balancedFromList (preOrderList t) == t

Also for any list xs we should have:

preOrderList (balancedFromList xs) == xs

balancedFromList [] = ILeaf
balancedFromList (x:xs) =
  IBranch x (balancedFromList ys) (balancedFromList zs)
  where
    n = length xs `div` 2
    ys = take n xs
    zs = drop n xs

main

This is here just in case we need a main function.

main :: IO ()
main = return ()

Source

Assignment 5 solutions