Notes week of 17 Sep

Assignment 1 tips

I’ll have the Assignment 1 solutions published in a few more days.

  • Q1 volumeSphere, Q2 quadratic: should be straightforward.

  • Q3 temperature conversion: you need an identifier for the function parameter on the left side of the equals. Must start with a lowercase letter. If you are getting failures, click through to figure out why. There could be compiler errors that offer useful hints.

  • Q4 Cartesian: just formulas, but you need to find them.

  • Q5 powerFast: you might get this to pass tests by defining square and then renaming powerSlow. But I will deduct a couple of points for that because it doesn’t take advantage of even exponents to speed up the calculation.

  • Q6 primes: One issue I saw here, that’s also common in C/C++ programs, is something like:

    This works, but it’s much more verbose than needed. If you’re returning True if an expression is true, and False otherwise, then you can just return the (Boolean) value of the expression:

List constructors

A single colon (:) is an operator for constructing a node in a linked list. The other constructor is an empty list, which is just designated as [].

The list syntax with brackets and commas is really just a short-hand

for applying these constructors:

[1,2,3,4] ↪
(1:(2:(3:(4:[])))) ↪
1:2:3:4:[]

With or without the parentheses, those expressions are the same because (:) is right-associative. Another way to think of this is that it builds the list nodes from back to front.

Each box is produced by one application of the list constructor (:).
Each box is produced by one application of the list constructor (:).
  • List append (++)
  • head, tail
  • take, drop

List patterns

When defining a function, instead of just a plain parameter name we an use a pattern. We saw this already for the simple case of pairs. Instead of defining:

and using fst p1 for the X value and snd p1 for the Y, we can replace each simple variable name with a pair:

This syntax is normally used for constructing pairs, but here it is for destructing (also known as matching) pairs.

We can use the list constructor similarly. Consider this definition:

Remember when we write a:b:c, it is grouped from the right (a:(b:c)). This is a pattern composed of list constructors. Thus we must call the function with a list argument. For example:

flarn [3,5,9,2]

To see how this argument will match the pattern, rewrite it using the list constructor and compare to the structure of the pattern:

  (3:(5:(9:(2:[]))))
  (a:(b:c         ))

So the pattern binds the parameter variables as follows:

  • a = 3
  • b = 5
  • c = 9:2:[] = [9,2]

Perform those replacements in the right-hand side of flarn and you can derive the result:

flarn [3,5,9,2] ↪ 3+5 ↪ 8

It may happen that the pattern does not match. Here’s an example:

flarn [8] ↪
flarn (8:[])

Match that argument against the pattern:

  (8:[]   )
  (a:(b:c))

and you realize that we’re trying to match the empty list [] with a list constructor (b:c). These do not match, so the call produces an error:

*** Exception: Non-exhaustive patterns in function flarn

You can define a function with multiple patterns (much like a function with multiple guards) by specifying separate equations with the same function name.

Here are some example functions, with derivations of function calls beneath them.

There are three clauses here, each with different patterns. The clause pattern are tried in order, and the first to match is executed. If none of the clauses match, then it throws the “Non-exhaustive patterns” error.

flub [9,1,5,2] ↪
  -- First clause matches with a=9, b=1, c=5, d=[2]
sum [2] + 9 - 1 + 5 ↪
2 + 9 - 1 + 5 ↪
11 - 1 + 5 ↪
10 + 5 ↪
15
flub [9,1,5] ↪
  -- First clause still matches, with a=9, b=1 c=5, d=[]
  -- (It's okay if a tail in a pattern is the empty list.)
sum [] + 9 - 1 + 5 ↪
  -- Sum of an empty list is zero.
0 + 9 - 1 + 5 ↪
9 - 1 + 5 ↪
8 + 5 ↪
13
flub [9,1] ↪
  -- This time, first clause doesn't match because c:d doesn't match []
  -- Second clause matches with a=9, b=[1]
sum [1] + 9 ↪
1 + 9 ↪
10
flub [9] ↪
  -- Again, second clause matches with a=9, b=[]
sum [] + 9 ↪
0 + 9 ↪
9
flub [] ↪
  -- Now first and second clauses don't match, but
  -- third clause does. No variables bound by that match.
99

Let’s try another function. This one returns a list, and doesn’t do arithmetic so it can operate on list of any type (including strings).

traal "cat" ↪
traal ('c':'a':'t':[]) ↪
  -- First clause matches with x = 'c', xs = 'a':'t':[] = "at"
'c' : 'c' : traal "at" ↪
  -- First clause matches with x = 'a', xs = 't':[] = "t"
'c' : 'c' : 'a' : 'a' : traal "t" ↪
  -- First clause matches with x = 't', xs = [] = ""
'c' : 'c' : 'a' : 'a' : 't' : 't' : traal [] ↪
  -- First clause doesn't match, but second does
'c' : 'c' : 'a' : 'a' : 't' : 't' : [] ↪
  -- The rest builds up list from back to front
'c' : 'c' : 'a' : 'a' : 't' : "t" ↪
'c' : 'c' : 'a' : 'a' : "tt" ↪
'c' : 'c' : 'a' : "att" ↪
'c' : 'c' : "aatt" ↪
'c' : "caatt" ↪
"ccaatt"

Implementing basic list operations

Many list operations, such as map, filter, and append (++) are built-in to Haskell (provided by the standard ‘prelude’), but it can be instructive to try to implement those ourselves. So here are versions of ++, map, and filter along with derivations that trace their behavior. They all work by recursively processing a list, handling the head element and then using a recursive call to provide the tail.

Append

The append operator (++) just concatenates two lists. It can be implemented like this:

myAppend [3,5] [2,7,9] ↪
  -- Neither list empty, so matches last clause
  -- with x=3, xs=[5], ys=[2,7,9]
3 : myAppend [5] [2,7,9] ↪
  -- Last clause with x=5, xs=[], ys=[2,7,9]
3 : 5 : myAppend [] [2,7,9] ↪
  -- Second clause, with ys=[2,7,9]
3 : 5 : [2,7,9] ↪
3 : [5,2,7,9] ↪
[3,5,2,7,9]

The first clause of myAppend, which requires that the right list is empty, is not actually necessary. It’s just an optimization. We’d get the same result without it, but have to do a lot more work.

myAppend [3,5] [] ↪
  -- Using first clause, this is finished immediately.
  -- But if we didn't have that, it would match last clause
  -- with x=3, xs=[5], ys=[]
3 : myAppend [5] [] ↪
  -- Again, without first clause it would match last
  -- with x=5, xs=[], ys=[]
3 : 5 : myAppend [] [] ↪
  -- Now it matches second clause
3 : 5 : [] ↪
3 : [5] ↪
[3,5]

Map

The map function applies a function to each element of a list, and returns a list of the results.

myMap square [3,7,5] ↪
  -- Matches second clause with f=square, x=3, xs=[7,5]
square 3 : myMap square [7,5] ↪
  -- Matches second clause with f=square, x=7, xs=[5]
square 3 : square 7 : myMap square [5] ↪
  -- Matches second clause with f=square, x=5, xs=[]
square 3 : square 7 : square 5 : myMap square [] ↪
  -- Matches first clause
square 3 : square 7 : square 5 : [] ↪
square 3 : square 7 : [25] ↪
square 3 : [49,25] ↪
[9,49,25]

Filter

The filter function applies a Boolean function to each element of a list and keeps only those elements for which the function returned True. We write this one with the usual two clauses for the empty and non-empty list, but then the non-empty case uses guards to check the Boolean result.

myFilter even [2,3,4] ↪
  -- Matches second case with f=even, x=2, xs=[3,4]
  -- so check guard expression: even 2 ↪ True
2 : myFilter even [3,4] ↪
  -- Matches second case with f=even, x=3, xs=[4]
  -- so check guard expression: even 3 ↪ False
  -- thus it uses the otherwise case and ignores x.
2 : myFilter even [4] ↪
  -- Matches second case with f=even, x=4, xs=[]
  -- so check guard expression: even 4 ↪ True
2 : 4 : myFilter even [] ↪
  -- Matches first case
2 : 4 : [] ↪
2 : [4] ↪
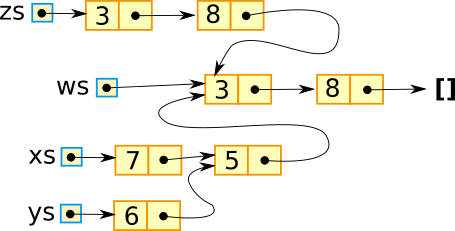
[2,4]

Structure sharing and garbage collection

Because each list node is immutable once created, multiple lists can have tails in common
Because each list node is immutable once created, multiple lists can have tails in common

List comprehensions

This is a syntax for creating, mapping, and filtering lists. Read the following as “the list of squares of x, where x comes from [2..5]”.

ghci> [square x | x <- [2..5]]
[4,9,16,25]

It is exactly equivalent to using map like this:

ghci> map square [2..5]
[4,9,16,25]

The expression with the left arrow (x <- [2..5]) is called a generator. You can have multiple generators in this area, and also Boolean expressions, all separated by commas. Here is an example with one generator and one Boolean filter:

ghci> [square x | x <- [2..5], odd x]
[9,25]

It’s the same as:

ghci> map square (filter odd [2..5])
[9,25]

It gets more interesting when you add multiple generators. Then it treats them like nested loops:

ghci> [x+y | x <- [1..3], y <- [4..6]]
[5,6,7,6,7,8,7,8,9]

The numbers it is generating can be explained as this iteration of x and y:

1+4 = 5
1+5 = 6
1+6 = 7
2+4 = 6
2+5 = 7
2+6 = 8
3+4 = 7
3+5 = 8
3+6 = 9

Here’s a nice example of generating Pythagorean triples in a particular range:

ghci> range = [1..100]
ghci> [(a,b,c) | a<-range, b<-range, a<b, c<-range, c^2==a^2+b^2]
[(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,12,15),(9,40,41),
(10,24,26),(11,60,61),(12,16,20),(12,35,37),(13,84,85),(14,48,50),
(15,20,25),(15,36,39),(16,30,34),(16,63,65),(18,24,30),(18,80,82),
(20,21,29),(20,48,52),(21,28,35),(21,72,75),(24,32,40),(24,45,51),
(24,70,74),(25,60,65),(27,36,45),(28,45,53),(28,96,100),(30,40,50),
(30,72,78),(32,60,68),(33,44,55),(33,56,65),(35,84,91),(36,48,60),
(36,77,85),(39,52,65),(39,80,89),(40,42,58),(40,75,85),(42,56,70),
(45,60,75),(48,55,73),(48,64,80),(51,68,85),(54,72,90),(57,76,95),
(60,63,87),(60,80,100),(65,72,97)]

Following is just needed to make this Literate Haskell file executable.

Source