Assignment 7 specification

Tue Oct 30

In this assignment, we’ll define a small language of arithmetic expressions that can be interpreted and compiled into lower-level instructions.

Numeric operators

Let’s begin with binary and unary operators. You have seen these enumerated types previously, but we’ll also define how to interpret them.

Here is a tiny interpreter that converts each unary operator into one of the Haskell numeric functions. The Abs constructor is implemented using the abs function, which has the required type Double -> Double. The Neg constructor is implemented using an operator section of the subtraction operator: to negate a value, you subtract it from zero.

Here are some examples of its usage:

ghci> runUnaryOp Sqrt 25
5.0
ghci> runUnaryOp Abs (-10)
10.0
ghci> runUnaryOp Neg (10)
-10.0
ghci> runUnaryOp Neg (-10)
10.0

Now for the binary operators.

We can similarly define what these do by translating each to a Haskell numeric function. These are all operator sections. The first few are done for you:

Some sample uses:

ghci> runBinaryOp Add 3 5
8.0
ghci> runBinaryOp Pow 2 12
4096.0
ghci> runBinaryOp Sub 10 15
-5.0
ghci> runBinaryOp Mul 10 15
150.0

Expression trees

As presented in class, arithmetic expressions are trees. Here is a type defining a tree in which we can have literal numbers, variable names, and both kinds of operators.

To evaluate expression trees, we need an environment that provides values for any variables that may be present in the tree. Evaluation can produce an error only if it encounters a variable not present in the environment. We’ll represent the environment as a list of pairs:

Some sample environments:

This evaluator differs from the one we did in class by returning an Either type where the Left value represents the name of an unknown variable.

We’ll do the recursive cases first. We evaluate one or both subtrees recursively, and then apply the runUnaryOp or runBinaryOp as needed. I will explain the <$> and <*> more thoroughly in class, but they allow us to apply the appropriate run function within a functor (such as Either or Maybe).

Now we need clauses for the two base cases: the Num and Var constructors. These will construct either a Right value carrying a number, or Left value carrying the name of an unknown variable. (Use case and lookup to access the environment.)

Sample expressions

Formula for the area of a circle: \(\pi r^2\)

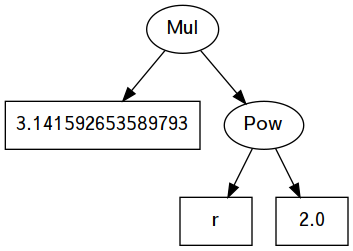
ghci> evaluate [] egCircle
Left "r"
ghci> evaluate [("r",8)] egCircle
Right 201.06192982974676
ghci> evaluate [("r",2.22)] egCircle
Right 15.483025233951938

Here is an expression for the Pythagorean theorem (Euclidean distance): \(\sqrt{x^2 + y^2}\)

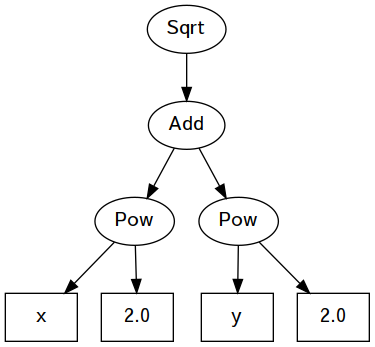
ghci> evaluate [] egEuclid
Left "x"                   -- Encountered unknown variable 'x'
ghci> evaluate [("x",8)] egEuclid
Left "y"                   -- Encountered unknown variable 'y'
ghci> evaluate [("x",8),("y",5)] egEuclid
Right 9.433981132056603    -- Correct answer
ghci> evaluate [("x",3),("y",4)] egEuclid
Right 5.0                  -- Correct answer

Next example is one arm of the quadratic formula:

\[\frac{ -b + \sqrt{b^2-4ac} }{2a}\]

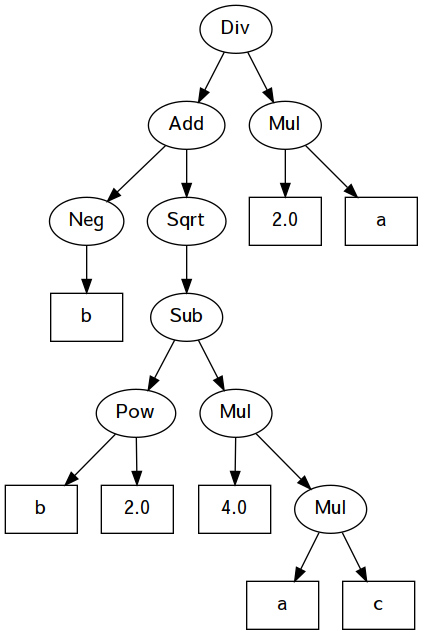
These are some of the exact test cases I used for our implementation of the quadratic formula in assignment 1:

ghci> evaluate [] egQuadratic
Left "b"
ghci> evaluate [("a",2),("b",9),("c",3)] egQuadratic
Right (-0.36254139118231254)
ghci> evaluate [("a",1),("b",-1),("c",-1)] egQuadratic
Right 1.618033988749895
ghci> evaluate [("a",2),("b",8),("c",6)] egQuadratic
Right (-1.0)
ghci> evaluate [("a",1),("b",30),("c",pi)] egQuadratic
Right (-0.1050878704703262)

Finally, here is the Manhattan distance, using absolute value: \(|x1-x2|+|y1-y2|\)

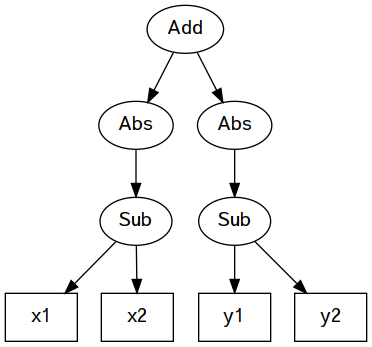
And here are some of the test cases on Manhattan distance from assignment 1:

ghci> evaluate [("x1",3),("y1",2),("x2",9),("y2",2)] egManhattan
Right 6.0
ghci> evaluate [("x1",-3),("y1",-4),("x2",-8),("y2",9)] egManhattan
Right 18.0
ghci> evaluate [("x1",0),("y1",0),("x2",1),("y2",1)] egManhattan
Right 2.0
ghci> evaluate [("x1",3),("y1",6.1),("x2",3),("y2",2)] egManhattan
Right 4.1

A stack machine

Now we’re going to consider a very different way of evaluating arithmetic expressions. Instead of interpreting operations in a tree format, this one follows a sequence of instructions and uses a stack for temporary memory. This is a lot more like executing assembly language or machine code.

Here is a sample program (not in Haskell notation) for a stack machine, and a trace of its stack when x=3 and y=4.

Instructions:    Stack (grows to the right):
                    ε (empty)
  LOAD x           3
  PUSH 2           3   2
  POW              9
  LOAD y           9   4
  PUSH 2           9   4    2
  POW              9   16
  ADD              25
  PUSH 0.5         25  0.5
  POW              5

Each instructions pushes and/or pops values from the stack:

  • LOAD retrieves the value of a variable from the environment, and pushes it onto the stack.

  • PUSH pushes a literal number onto the stack.

  • POW and other binary operators pop the top two elements from the stack, execute the operation, and then push the result.

So here is one way to represent instructions as a Haskell data type:

We allow any BinaryOp to be an instruction. We could do the same for UnaryOp, but instead let’s compile away the Sqrt and Neg, and only provide one unary instruction: Abso for absolute value. To do square root and negation, we just use these equivalences in terms of Pow and Sub:

  • \(\sqrt{x} = x^{0.5}\)
  • \(-x = 0 - x\)

So the sample stack program above would be represented as a list of instructions, like this:

When evaluating trees, there was one kind of error: a missing variable. So we had the tree evaluator return Either String Double, where the String indicated the name of the missing value.

When executing a list of instructions, there can be two kinds of errors: a missing variable, and also a stack underflow. Underflow happens when an instruction needs more operands than are available on the stack. Consider this program:

Instructions:    Stack (grows to the right):
                    ε (empty)
  PUSH 3            3
  PUSH 4            3  4
  PUSH 5            3  4  5
  MUL               3  20
  ADD               23
  POW              *UNDERFLOW*

When the program reaches the POW instruction, it requires two operands on top of the stack, but there is only one. So an underflow error occurs.

We’ll represent our two types of errors using a data type:

In Haskell, we’ll just represent the stack as a list of numbers. Prepend with the list constructor (:) to push. Pattern-match the head element(s) to pop.

Now we’re ready to define the execution of our stack machine. It takes an environment, an initial stack, and a list of instructions. It returns a resulting stack, or else an error.

If there are no instructions left to execute, just return the stack:

A push instruction adds a value to the stack, and continues with subsequent instructions:

A binary operator pattern-matches to find two values on the top of the stack, and then applies the operator, pushes the result, and continues with subsequent instructions:

TODO: There are still three clauses for you to complete:

  • computing the absolute value

  • loading a variable from the environment, or reporting MissingVar if it’s not available.

  • reporting a StackUnderflow if there weren’t enough arguments on the stack for Bop or Abso.

Executing some small sample programs:

ghci> execute [] [] [Push 8]
Right [8.0]
ghci> execute [] [] [Load "x"]
Left (MissingVar "x")
ghci> execute [] [] [Bop Pow]
Left (StackUnderflow (Bop Pow))
ghci> execute [] [] [Push 3, Push 4, Bop Div]
Right [0.75]
ghci> execute [] [] [Push (-8), Abso]
Right [8.0]
ghci> execute [] [] [Push 9, Abso]
Right [9.0]
ghci> execute [("x",4)] [] [Load "x"]
Right [4.0]
ghci> execute [("x",4)] [] [Load "x", Load "x", Bop Mul]
Right [16.0]

A compiler!

There are no more tasks for you to complete in this section, but we’re going to do something pretty amazing. We’re going to compile (translate) the expression trees into a list of stack machine instructions. The type of the compiler says exactly that:

The base cases are pretty easy:

Unary operators are ‘compiled away’ either by converting them to binary operators:

or using the Abso instruction:

And binary operators are compiled quite simply like this:

Check it out — here are compiled programs for the three sample trees:

ghci> compile egEuclid
[Load "x", Push 2.0, Bop Pow,
 Load "y", Push 2.0, Bop Pow,
 Bop Add, Push 0.5, Bop Pow]
ghci> compile egQuadratic
[Push 0.0, Load "b", Bop Sub, Load "b", Push 2.0, Bop Pow,
 Push 4.0, Load "a", Load "c", Bop Mul, Bop Mul, Bop Sub,
 Push 0.5, Bop Pow, Bop Add, Push 2.0, Load "a", Bop Mul, Bop Div]
ghci> compile egManhattan
[Load "x1", Load "x2", Bop Sub, Abso,
 Load "y1", Load "y2", Bop Sub, Abso, Bop Add]

And we can execute those programs in given environments, and produce the same result as the evaluator:

ghci> evaluate [("x1",-3),("y1",-4),("x2",-8),("y2",9)] egManhattan
Right 18.0
ghci> execute [("x1",-3),("y1",-4),("x2",-8),("y2",9)] [] (compile egManhattan)
Right [18.0]
ghci> evaluate [("a",2),("b",9),("c",3)] egQuadratic
Right (-0.36254139118231254)
ghci> execute [("a",2),("b",9),("c",3)] [] (compile egQuadratic)
Right [-0.36254139118231254]
ghci> evaluate [("x",8),("y",5)] egEuclid
Right 9.433981132056603
ghci> execute [("x",8),("y",5)] [] (compile egEuclid)
Right [9.433981132056603]

You also get the same error results if there are unused variables.

ghci> evaluate [("k",9)] egEuclid
Left "x"
ghci> execute [("k",9)] [] (compile egEuclid)
Left (MissingVar "x")

A correctly-compiled expression tree should never produce a StackUnderflow.