Notes week of 8 Oct

Imports must go at the top of your Haskell file, before any definitions.

Assignment 4 tips

To pull the Just values out of the list in catMaybes, you want to pattern-match on them. The usual recursion structure for a list has two cases, for empty and the list constructor:

But for this problem we can subdivide the cons case further, to test whether the head element is Nothing or Just:

Fill in all the dotted expressions and you should be able to get this to work.

Bounded stack data type

The built-in lists work pretty well as a stack if pushing and popping happen at the head of the list. But here we also store an integer capacity to tell us how many elements we are allowed to push.

Create a new, empty stack with a given capacity.

Push onto a stack – can fail if the remaining capacity is zero. Otherwise it subtracts one from the capacity and the push succeeds.

Pop the stack can fail if the stack is empty.

Top returns the value on top, and can fail if the stack is empty.

In all of these, failure is represented by the Nothing value.

ghci> new 2
BoundedStack {capacity = 2, elements = []}
ghci> push 5 (new 2)
Just (BoundedStack {capacity = 1, elements = [5]})
ghci> push 5 (new 0)
Nothing
ghci> pop (new 2)
Nothing

(The last push failed because the capacity of the stack was zero. The pop failed because the stack was empty.)

Since the push/pop functions return Maybe, we can sequence them using the monadic composition operators (>=>) (left-to-right composition) or (<=<) (right-to-left):

ghci> (push 5 >=> push 3 >=> push 2) (new 4)
Just (BoundedStack {capacity = 1, elements = [2,3,5]})
ghci> (push 5 <=< push 3 <=< push 2) (new 4)
Just (BoundedStack {capacity = 1, elements = [5,3,2]})
ghci> (push 5 <=< push 3 <=< push 2) (new 2)
Nothing

Functor type class

Functor is a type class representing types T which have a map-like operation with this type:

There are a lot of choices for the T type; some built-in examples are lists, Maybe, and Either:

We can declare that our own data types should implement type classes like Functor using this instance keyword:

We made BoundedStack a functor by defining the fmap function on it. Its type is:

The definition of fmap for BoundedStack looks like it’s recursive – it uses fmap on the right side of the equals. But it actually isn’t recursive, because that fmap is the one defined on lists. So we implement fmap on BoundedStack by using fmap on the list component. (The capacity just stays the same.)

The treeMap function I specified in Assignment 4 can be used to turn the Tree data type into a functor. You can see it has the correct type:

Here is how you would define it (I’m leaving the actual definition of each case out with the error function.)

Bifunctor type class

The Functor instance of the Either type only applies to the Right value, which you can see from its type:

(The type variable c is left unchanged.)

ghci> fmap succ (Left 8)
Left 8
ghci> fmap succ (Right 8)
Right 9
ghci> fmap succ (Left "Hello world")
Left "Hello world"

There are a few type constructors like Either that take two type arguments. To apply a function to both sides, there is the type class Bifunctor and its method bimap. The function has this type, for some type T:

So it takes two functions, which can be applied to the two potential values. Both Either and the pair type (a,b) are Bifunctors. Here is the type signature of bimap specialized to those types:

And its usage:

ghci> bimap square succ (Left 4)
Left 16
ghci> bimap square succ (Right 4)
Right 5
ghci> bimap square succ (4,5)
(16,6)

Our previously-defined tree type only carries values at its leaves. Here is a variation that can carry values (of different types) at branches and at leaves.

And I can specify that its a Bifunctor by instantiating bimap like this:

ghci> bimap square succ t1
BBranch 81 (BLeaf 'D') (BBranch 121 (BLeaf 'Y') (BLeaf 'H'))

The above use of bimap keeps the same tree structure, but applies square to the branch values and succ to the leaf values.

In GHCi, if we type :i Bifunctor you can see more of its definition and instances:

This shows that you can instantiate Bifunctor either by defining bimap or by defining first and second. Whichever choice you make, you get the other one for free. So first and second will work on BTree as well, applying a function to branches or leaves (respectively), and leaving the other alone.

ghci> first succ t1
BBranch 10 (BLeaf 'C') (BBranch 12 (BLeaf 'X') (BLeaf 'G'))
ghci> first square t1
BBranch 81 (BLeaf 'C') (BBranch 121 (BLeaf 'X') (BLeaf 'G'))
ghci> second succ t1
BBranch 9 (BLeaf 'D') (BBranch 11 (BLeaf 'Y') (BLeaf 'H'))

Monoid type class

A type is a Monoid if it has a distinguished “empty” value (sometimes called the identity) and an “append” operator for combining two values:

ghci> :i Monoid
class Monoid a where
  mempty :: a
  mappend :: a -> a -> a
  mconcat :: [a] -> a

Additionally, monoids are expected to obey these laws:

  • mappend mempty x = x (Left identity)
  • mappend x mempty = x (Right identity)
  • mappend (mappend x y) z = mappend x (mappend y z) (Associativity)

Lists are monoids, where the identity is the empty list and append function is the usual list concatenation:

ghci> mempty :: [Int]
[]
ghci> mappend mempty [1..5]
[1,2,3,4,5]
ghci> mappend [2..8] mempty
[2,3,4,5,6,7,8]
ghci> mappend [1..4] [6..10]
[1,2,3,4,6,7,8,9,10]

There are many other instances of monoids, and we can define our own. Maybe types are monoids if the contained type is also a monoid:

ghci> mempty :: Maybe String
Nothing
ghci> mappend mempty (Just "Hello")
Just "Hello"
ghci> mappend (Just "Hello") mempty
Just "Hello"
ghci> mappend (Just "Hello") (Just "World")
Just "HelloWorld"

Notice how when there are two Just values, it appends those together in the result. That’s why the value inside the Maybe needs to be a monoid too.

Numbers have several operations that obey the monad laws: addition with the identity zero, or multiplication with the identity one. Since it would be ambiguous which of the monoids we want, numeric types are not monoids all on their own:

ghci> mempty :: Int
error:
    • No instance for (Monoid Int) arising from a use of ‘mempty’
ghci> mappend (Just 3) (Just 4) :: Maybe Int
error:
    • No instance for (Monoid Int) arising from a use of ‘mappend’

However if you import Data.Monoid you will have access to the types Sum and Product which wrap numeric types to provide the appropriate identities and appends:

ghci> mempty :: Product Int
Product {getProduct = 1}
ghci> mappend 3 5 :: Product Int
Product {getProduct = 15}
ghci> mempty :: Sum Int
Sum {getSum = 0}
ghci> mappend 3 5 :: Sum Int
Sum {getSum = 8}

Here is a tree that stores values only at interior branches.

A consequence of this definition is that leaves don’t carry any value at all, and therefore (unlike the previous tree definition) we can have a completely empty tree. Thus it’s a good candidate for a Monoid instance.

Like the Maybe instance, we require that the values carried by the tree are also monoids. Here is an example of how this monoid instance works, with diagrams of the trees.

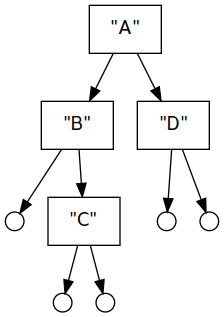
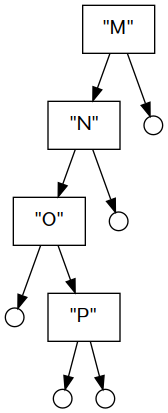
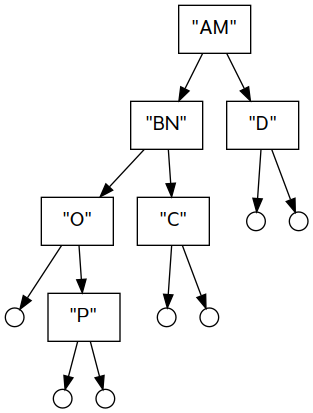
main

Source