We looked at creating new types and constructors with the data keyword. These types are often referred to as algebraic data types. Both types and constructors must begin with uppercase letters.

Enumerations

The simplest kind is an enumeration, where you just list all the possible values of the type. For example:

data ColorPalette
  = Red
  | Orange
  | Blue
  | Yellow
  | Green
  | Purple
  deriving (Eq, Enum, Ord, Show)

The deriving line is optional, but provides a list of type classes that the new type should implement. Certain built-in classes can be derived automatically this way. For other classes, you must specify the implementation. Here’s what the classes derived for ColorPalette mean:

Eq just means that you can compare two members of ColorPalette using operators (==) and (/=) (not equals):
```
ghci> Red == Blue
False
ghci> Red /= Blue
True
```
Ord generates an ordering of the members of ColorPalette so you can compare them with operators like (<) and (>). The ordering is just as given, so we have:
```
ghci> Red < Orange
True
ghci> Blue > Yellow
False
```
Show is a lot like the toString method on Java objects. It provides a way for the programmer or the GHCi system to convert objects to strings, for example to produce output. The corresponding function is show, but this is also implicitly used by the print function:
```
ghci> show Blue
"Blue"
ghci> print Blue
Blue
```
Enum just means that members of the ColorPalette class can be converted to and from integers. Here it’s done in the obvious way where the first member (Red) is zero, and then you count up from there.
```
ghci> fromEnum Red
0
ghci> fromEnum Yellow
3
```
When converting from integers back to members of ColorPalette, you need to specify the target type using :: if it can’t be inferred from context – without that it is assumed to be something different and these examples wouldn’t work:
```
ghci> toEnum 0 :: ColorPalette
Red
ghci> toEnum 3 :: ColorPalette
Yellow
ghci> toEnum 6 :: ColorPalette
*** Exception: toEnum{ColorPalette}: tag (6) is outside of
enumeration's range (0,5)
```

You can also define your own functions that accept or produce members of ColorPalette, such as this one to answer whether the color is considered to be primary:

isPrimary1 x = x == Red || x == Green || x == Blue

That definition relies on the Eq instance of ColorPalette, because it’s using (==) to compare two colors. If you don’t want to use Eq, you could instead write it with pattern-matching like this:

isPrimary2 Red = True
isPrimary2 Green = True
isPrimary2 Blue = True
isPrimary2 _ = False

Constructors with data

In using data for an enumeration, the constructors stand as values on their own. Now we’ll do an example where the constructor takes parameters, so that it associates some data with the value.

For this example, there are two different ways to represent points in a two-dimensional space: the Cartesian coordinate system, or polar coordinates. We’ll turn those into two alternates of the Coord data type.

data Coord
  = Cartesian {x, y :: Float}
  | Polar {angle, radius :: Float}
  deriving (Show)

Now you can create a value of type Coord using the constructor as a function, and providing its arguments. You can either use normal function notation (just separating the arguments with spaces), or use the record notation with curly braces. The difference is only whether the order matters:

ghci> Cartesian 3 4
Cartesian {x = 3.0, y = 4.0}
ghci> Cartesian {x=3, y=4}
Cartesian {x = 3.0, y = 4.0}
ghci> Cartesian {y=4, x=3}
Cartesian {x = 3.0, y = 4.0}
ghci> Cartesian 4 3
Cartesian {x = 4.0, y = 3.0}

Here’s a function that takes a coordinate in either notation, and ensures that it returns a coordinate in Cartesian notation. (So the constructor of the result will never be Polar.)

toCartesian :: Coord -> Coord
toCartesian (Cartesian x y) = Cartesian x y  -- nothing to do
toCartesian (Polar a r) = Cartesian x y
  where x = r * cos a
        y = r * sin a

ghci> toCartesian (Cartesian 3 4)
Cartesian {x = 3.0, y = 4.0}
ghci> toCartesian (Polar 3 4)
Cartesian {x = -3.95997, y = 0.56448}
ghci> toCartesian (Cartesian 1 1)
Cartesian {x = 1.0, y = 1.0}
ghci> toCartesian (Polar (pi/4) (sqrt 2))
Cartesian {x = 0.99999994, y = 0.99999994}

The last two entries in the above transcript show that the Cartesian coordinate \((1,1)\) is equal (within some tolerance for the approximations involved in floating-point computations) to the Polar coordinate \((\frac\pi4, \sqrt{2})\).

Now let’s do a distance calculation. For two Cartesian coordinates, this is the formula:

distance :: Coord -> Coord -> Float
distance (Cartesian x1 y1) (Cartesian x2 y2) =
  sqrt((x1-x2)^2 + (y1-y2)^2)

But we would apply a different formula if there are two polar coordinates:

distance (Polar a1 r1) (Polar a2 r2) =
  sqrt(r1^2 + r2^2 - 2*r1*r2*cos(a1-a2))

Finally, what if the coordinates are mismatched? We could force them into one or the other, and then apply distance again. Since we already wrote toCartesian, we’ll apply it to both coordinates.

distance c1 c2 =
  distance (toCartesian c1) (toCartesian c2)

Here are some sample Cartesian coordinates we can use:

p1 = Cartesian 1 1
p2 = Cartesian 2 2
q1 = Polar (pi/4) (sqrt 2)
q2 = Polar (pi/4) (2 * sqrt 2)

Recursive types

List type

Here is a variant of the built-in list type. It’s recursive because the definition of IntList refers to IntList in its Cons constructor. This is less flexible than the actual built-in list because it’s monomorphic – the elements of the list must have type Int.

data IntList
  = Empty
  | Cons {hd :: Int, tl :: IntList}
  deriving (Show)

This function is essentially like the built-in sum, but defined recursively on our own IntList type. Notice how the structure of the recursive function nicely matches the structure of the recursive type.

addList :: IntList -> Int
addList Empty = 0
addList (Cons h t) = h + addList t

Tree type

Here we define the type of a binary tree. Data can be held at both the branches (interior nodes) and leaves. The type variable lv stands for the type of values stored at the leaves. The type variable bv stands for the type of values stored at the branches.

data Tree lv bv
  = Leaf   {leafValue :: lv}
  | Branch {branchValue :: bv, left, right :: Tree lv bv}
  deriving (Show)

Here’s how we can compose those constructors to make a concrete tree – in this case, one where the branch type is Int and the leaf type is Char.

example1 =
  Branch 1
    (Branch 3 (Leaf 'A') (Leaf 'B'))
    (Branch 5 (Leaf 'C') (Leaf 'D'))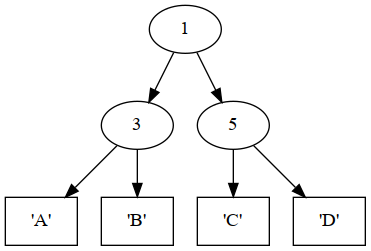

The tree defined by example1

Recursively count how many leaves are in the tree.

countLeaves :: Tree lv bv -> Int
countLeaves (Leaf _) = 1
countLeaves (Branch _ left right) =
  countLeaves left + countLeaves right

Assuming that the leaf type is integers, add the values at all the leaves.

addLeaves (Leaf x) = x
addLeaves (Branch _ left right) =
  addLeaves left + addLeaves right

An example tree with integers at the leaves.

example2 =
  Branch 'A'
    (Leaf 3)
    (Branch 'B'
      (Branch 'C'
        (Leaf 4)
        (Branch 'D'
          (Leaf 5)
          (Leaf 7)))
    (Leaf 9))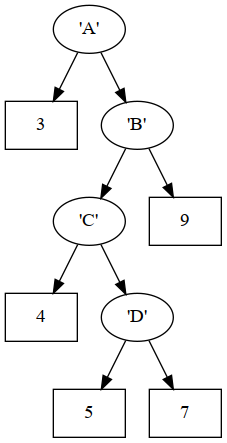

The tree defined by example2

So we can call addLeaves on example2, but it would be a type error to call it on example1.

ghci> addLeaves example2
28
ghci> addLeaves example1
<interactive>:1309:1-18: error:
    • No instance for (Num Char) arising from a use of ‘addLeaves’
    • In the expression: addLeaves example1
      In an equation for ‘it’: it = addLeaves example1

Main program

I’m not using this for anything, but if you compile this with runghc, it requires a main, so here it is.

main = return ()

PDF

Source

Code examples from 9/21 — data types