For this assignment, you will write some functions for processing tree data types in Haskell. Save all your functions into one file called a03.hs and submit it to this dropbox.

At the bottom of this document is a main program that I will use to test your code. You may paste it into your program and test that way too, by invoking main in GHCi, or using stack runghc on the filename. The main program contains one line (createGraphs) that won’t work; just remove it. Like in the previous assignment, if you get errors on the imports in the test driver, you need to stack install mtl.

Generic tree operations

In class we developed this tree type. The type variable lv stands for the type of values stored at the leaves. The type variable bv stands for the type of values stored at the branches.

data Tree lv bv
  = Leaf {leafValue :: lv}
  | Branch {branchValue :: bv, left, right :: Tree lv bv}
  deriving (Show, Eq)

Here is an example tree defined using the datatype. Compare it to the figure labeled with tree1.

tree1 =
  Branch 1                             -- Root
    (Branch 3 (Leaf 'A') (Leaf 'B'))   -- Left of root
    (Branch 5 (Leaf 'C') (Leaf 'D'))   -- Right of root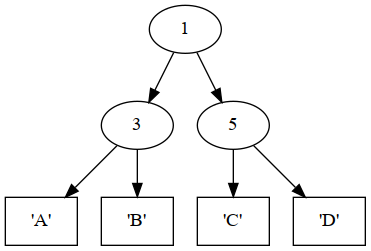

The tree defined by tree1

In tree1, the branch type is Int while the leaf type is Char. So we can declare its type signature like this:

tree1 :: Tree Char Int

Here is the definition of a more sophisticated tree structure, along with its diagram. The types are switched around, so we have integers at leaves and characters on the branches.

tree2 :: Tree Int Char
tree2 =
  Branch 'A'
    (Leaf 3)
    (Branch 'B'
      (Branch 'C'
        (Leaf 4)
        (Branch 'D'
          (Leaf 5)
          (Leaf 7)))
      (Leaf 9))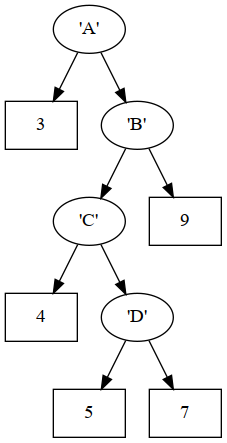

The tree defined by tree2

Now let’s define some generic functions on trees. They should work for trees containing any types of values.

(1) depth

The function depth should recursively calculate the depth (sometimes called height) of a tree. Leaves have depth zero. Each branch adds one level of depth to the max depth of its children. So for example:

depth (Leaf 8) ⇒ 0
depth tree1 ⇒ 2
depth tree2 ⇒ 4

Use this signature:

depth :: Tree lv bv -> Int

(2) listLeaves

The function

listLeaves :: Tree lv bv -> [lv]

should produce a list of all the leaves encountered by traversing the tree from left to right. You may want to use the list concatenation operator, which is ++. For example:

[3,4,5] ++ [6,7] ⇒ [3,4,5,6,7]
listLeaves (Leaf "Carl") ⇒ ["Carl"]
listLeaves tree1 ⇒ "ABCD"
listLeaves tree2 ⇒ [3,4,5,7,9]

(3) mirrorTree

The function

mirrorTree :: Tree lv bv -> Tree lv bv

should take a tree and produce a new tree that’s the same as the old one except all branches have their left and right children switch places. For example:

ghci> mirrorTree (Leaf 9)        -- Nothing changes on a leaf
Leaf {leafValue = 9}
ghci> mirrorTree (Branch 9 (Leaf 8) (Leaf 7))  -- The 8,7 change places
Branch {branchValue = 9,
        left = Leaf {leafValue = 7},
        right = Leaf {leafValue = 8}}
ghci> mirrorTree tree1
Branch {branchValue = 1,
        left = Branch {branchValue = 5,
                       left = Leaf {leafValue = 'D'},
                       right = Leaf {leafValue = 'C'}},
        right = Branch {branchValue = 3,
                        left = Leaf {leafValue = 'B'},
                        right = Leaf {leafValue = 'A'}}}

The next two figures illustrate the mirrors of tree1 and tree2.

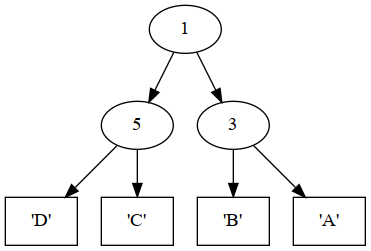
Result of mirrorTree tree1

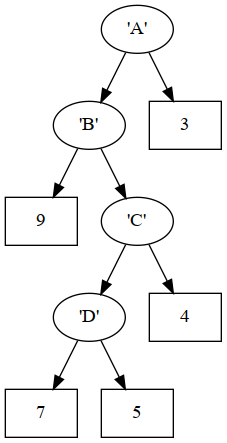
Result of mirrorTree tree2

(4) mapLeaves

The function

mapLeaves :: (lv1 -> lv2) -> Tree lv1 bv -> Tree lv2 bv

should take a function and a tree, and produce a new tree where the function has been applied to each leaf value. (This is similar to the map function on lists, but retains the structure of the tree.) Examples:

ghci> mapLeaves (+5) (Leaf 2)
Leaf {leafValue = 7}
ghci> mapLeaves (++ ", PhD") (Branch 5 (Leaf "Alice") (Leaf "Bob"))
Branch {branchValue = 5,
        left = Leaf {leafValue = "Alice, PhD"},
        right = Leaf {leafValue = "Bob, PhD"}}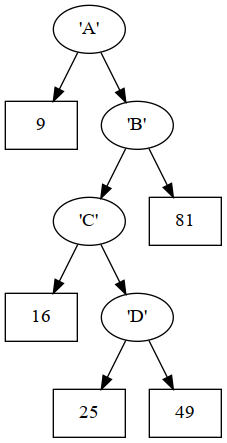

Result of mapLeaves (^2) tree2

(5) mapBranches

mapBranches :: (bv1 -> bv2) -> Tree lv bv1 -> Tree lv bv2

This function should take a function and a tree, and produce a new tree where the function has been applied to each branch value, preserving the structure of the tree. Examples:

ghci> mapBranches (*2) (Leaf 9)
Leaf {leafValue = 9}
ghci> mapBranches (*2) (Branch 9 (Leaf 15) (Leaf 28))
Branch {branchValue = 18,
        left = Leaf {leafValue = 15},
        right = Leaf {leafValue = 28}}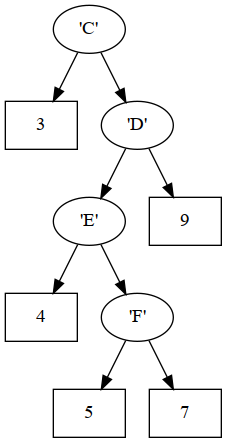

Result of mapBranches (succ . succ) tree2 where the successor function (succ) applied to characters produces the next character

Arithmetic expression trees

Now we will explore a particular use case for trees: to represent arithmetic expressions. That is, expressions containing numbers and arithmetic operations like add, subtract, multiply, etc.

First let’s enumerate a type for arithmetic operations:

data ArithOp = Add | Subtract | Multiply | Divide | Power
  deriving (Show, Eq)

Using the ArithOp type for the values at branches, and Float for the types of values at leaves, we can define an expression tree:

expr1 :: Tree Float ArithOp
expr1 =
  Branch Multiply
    (Branch Add (Leaf 1) (Leaf 2))
    (Leaf 3)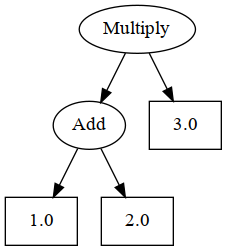

The expression tree defined by expr1

(6) calculate

calculate :: ArithOp -> Float -> Float -> Float

This function should take an ArithOp and two numbers, and applies the appropriate operator. Basically that means we are defining Add by using the + symbol, and Multiply by using the * symbol, etc. Here are some examples:

ghci> calculate Divide pi 2.5
1.2566371
ghci> calculate Add pi 2.5
5.641593
ghci> calculate Multiply pi 2.5
7.853982
ghci> calculate Subtract pi 2.5
0.64159274
ghci> calculate Power pi 2.5
17.49342

(7) interpret

interpret :: Tree Float ArithOp -> Float

This function should take a tree representing and arithmetic expression, and reduce it to a single floating-point number by applying all the operators to their operands as specified by the tree structure. For example, with the tree represented by expr1 we would produce steps like these:

(Multiply (Add 1.0 2.0) 3.0) ⇒
(Multiply 3.0 3.0) ⇒
9.0

ghci> interpret expr1
9.0
ghci> interpret (Leaf pi)
3.1415927
ghci> interpret (Branch Divide (Leaf pi) (Leaf 2))
1.5707964

(8) expr2

Define a variable expr2 which represents the arithmetic expression in the next figure.

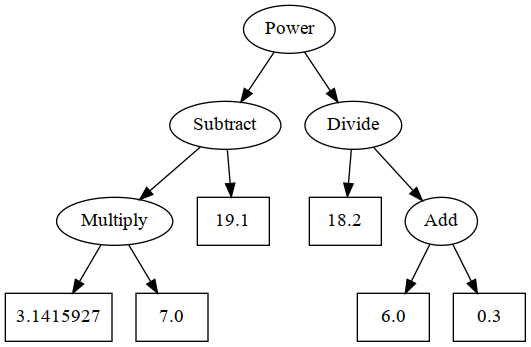
The expression tree defined by expr2

Some examples of its expected performance are in the test code.

Test code

import Control.Monad.RWS
import Control.Monad.State
import System.IO
main = do
  createGraphs  -- You can remove this line
  flip execStateT (0,0) $ do
    -- Ex 1 depth
    verify "1.01 depth" 2 $ depth tree1
    verify "1.02 depth" 4 $ depth tree2
    verify "1.03 depth" 2 $ depth expr1
    verify "1.04 depth" 0 $ depth (Leaf "a")
    -- Ex 2 listLeaves
    verify "2.01 listLeaves" "ABCD"      $ listLeaves tree1
    verify "2.02 listLeaves" [3,4,5,7,9] $ listLeaves tree2
    verify "2.03 listLeaves" [1,2,3]     $ listLeaves expr1
    verify "2.04 listLeaves" [99]        $ listLeaves $ Leaf 99
    -- Ex 3 mirrorTree
    verify "3.01 mirrorTree" "DCBA"      $ listLeaves $ mirrorTree tree1
    verify "3.02 mirrorTree" [9,7,5,4,3] $ listLeaves $ mirrorTree tree2
    verify "3.03 mirrorTree" [3,2,1]     $ listLeaves $ mirrorTree expr1
    verify "3.04 mirrorTree" [99]        $ listLeaves $ mirrorTree $ Leaf 99
    -- Ex 4 mapLeaves
    verify  "4.01 mapLeaves" "BCDE"          $ listLeaves $ mapLeaves succ tree1
    verify  "4.02 mapLeaves" "@ABC"          $ listLeaves $ mapLeaves pred tree1
    verify  "4.03 mapLeaves" [9,16,25,49,81] $ listLeaves $ mapLeaves (^2) tree2
    verifyF "4.04 mapLeaves" 22.245312 $ sum $ listLeaves $ mapLeaves (**2.5) expr1
    -- Ex 5 mapBranches
    verify "5.01 mapBranches" (Leaf 6) $ mapBranches (+1) (Leaf 6)
    verify "5.02 mapBranches" (Branch 9 (Leaf 6) (Leaf 7)) $
             mapBranches (+1) (Branch 8 (Leaf 6) (Leaf 7))
    -- Ex 6
    verifyF "6.01 calculate" (pi/2) $ calculate Divide   pi 2
    verifyF "6.02 calculate" (pi+2) $ calculate Add      pi 2
    verifyF "6.03 calculate" (pi*2) $ calculate Multiply pi 2
    verifyF "6.04 calculate" (pi-2) $ calculate Subtract pi 2
    verifyF "6.05 calculate" (pi^2) $ calculate Power    pi 2
    -- Ex 7
    verifyF "7.01 interpret"  9.0 $ interpret expr1
    verifyF "7.02 interpret" 27.0 $ interpret $ mapLeaves (+1.5) expr1
    verifyF "7.03 interpret"  6.0 $ interpret $ mapBranches (const Multiply) expr1
    -- Ex 8
    verify  "8.01 expr2" 3 $ depth expr2
    verify  "8.02 expr2" [pi,7,19.1,18.2,6,0.3] $ listLeaves expr2
    verifyF "8.03 expr2" 21.477394 $ interpret expr2
    verifyF "8.04 expr2" 21.480368 $ interpret $ mirrorTree expr2
    verifyF "8.05 expr2" 379.6297 $ interpret $ mapLeaves (+1) expr2
    verifyF "8.06 expr2" 53.741592 $ interpret $ mapBranches (const Add) expr2
  where
    say = liftIO . putStrLn
    correct (k, n) = (k+1, n+1)
    incorrect (k, n) = (k, n+1)
    verify :: (Show a, Eq a) => String -> a -> a -> StateT (Int,Int) IO ()
    verify = verify' (==)
    verifyF = verify' (\x y -> abs(x-y) < 0.00001)
    verify' :: (Show a) => (a -> a -> Bool) -> String -> a -> a ->
              StateT (Int,Int) IO ()
    verify' eq tag expected actual
      | eq expected actual = do
          modify correct
          say $ " OK " ++ tag
      | otherwise = do
          modify incorrect
          say $ "ERR " ++ tag ++ ": expected " ++ show expected
            ++ " got " ++ show actual
-- End of test driver

PDF

Assignment 3

Generic tree operations

(1) depth

(2) listLeaves

(3) mirrorTree

(4) mapLeaves

(5) mapBranches

Arithmetic expression trees

(6) calculate

(7) interpret

(8) expr2

Test code