Notes from 10/19

Zip

We spent some time on the zip and zipWith functions. zip takes two lists, and combines them into a list of pairs. In each pair, the first element comes from the first list, and the second element from the second list. The best way to understand is examples:

ghci> zip [1..5] [4..8]
[(1,4),(2,5),(3,6),(4,7),(5,8)]
ghci> zip "try" "now"
[('t','n'),('r','o'),('y','w')]

If one list is longer than the other, the leftover elements in the longer list are just ignored:

ghci> zip [1..5] [10..]
[(1,10),(2,11),(3,12),(4,13),(5,14)]

That example also illustrates that one (or both) of the lists can be infinite.

In addition to zipping together two lists, we may want to apply a function to the results. We can do this with just map and zip used together, but it’s a little awkward – we’d need the function passed to map to take a pair of arguments rather than two separate arguments. But here’s an example:

multiply (a,b) = a*b

ghci> map multiply $ zip [2..6] [4..]
[8,15,24,35,48]

These results represent \(2\times4\), then \(3\times5\), then \(4\times6\), etc. Now look at the type of our multiply function, and compare that to the type of the multiplication operator itself:

ghci> :t multiply
multiply :: Num a => (a, a) -> a
ghci> :t (*)
(*) :: Num a => a -> a -> a

The difference is that one takes its operands as a pair (a,a) and the other takes them separately. When using map with zip as above, we need the version that takes a pair.

An alternative is the function zipWith, which can map and zip at the same time, and so it uses functions with separate arguments. Then we can just pass (*) directly, without having to define multiply:

ghci> zipWith (*) [2..6] [4..]
[8,15,24,35,48]

The function passed to zipWith doesn’t need to be an operator, and also the types of the lists don’t have to match. Here’s an extended example to demonstrate those points:

copyChar :: Char -> Int -> String
copyChar c n = take n $ repeat c

The function repeat takes a value and produces in infinite list containing copies of that value. So if we only take n, it represents n copies of c:

ghci> copyChar 'c' 5
"ccccc"
ghci> copyChar '$' 3
"$$$"

Now I can use copyChar in zipWith as follows:

ghci> zipWith copyChar "abcde" [1..]
["a","bb","ccc","dddd","eeeee"]
ghci> zipWith copyChar "abcde" $ repeat 4
["aaaa","bbbb","cccc","dddd","eeee"]
ghci> zipWith copyChar "abcde" $ [5,4..]
["aaaaa","bbbb","ccc","dd","e"]

More lazy examples

We revisited the example of recursively generating the infinite list of Fibonacci numbers. Here’s the code, and a diagram that helps explain what is happening:

fibs :: [Integer]
fibs = 1 : 1 : zipWith (+) fibs (tail fibs)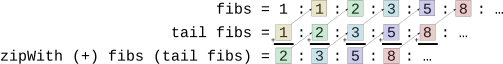

How fibs is calculated.

The light arrows connecting same-colored boxes indicate that those all represent the same location in memory, so calculating one completes the connected ones too.

Here’s another problem that we can solve with a similar technique. Suppose we want the running sums of a (potentially infinite) list of numbers. So given input [3,8,10] the output would be [0,3,11,21]. The result starts with zero because it’s the additive identity. Then it adds one element at a time from the input list. Zero plus 3 is 3; then add 8 to get 11; then add 10 to get 21.

ghci> runningSums [3,8,10]
[0,3,11,21]
ghci> take 10 $ runningSums [2..]
[0,2,5,9,14,20,27,35,44,54]

Here’s the definition and graphical explanation.

runningSums xs = 0 : zipWith (+) xs (runningSums xs)

How runningSums [2..] is calculated.

Threading state

Random

Many languages have a function like rand() or random() that just returns a (pseudo-)random number of some kind. Here’s an example in Python – it returns a random floating-point number between 0 and 1:

 >>> from random import random
 >>> random()
 0.9842441059136995
 >>> random()
 0.09433094029944189
 >>> random()
 0.7783129433643198
 >>> random()
 0.3644603595589918
 >>> [random(), random(), random()]
 [0.6033139138336018, 0.640450866910694, 0.3319755729652476]

A function like this is not pure. Purity means that a function depends only on its inputs, and cannot rely on other side effects. The call random() takes no inputs, so purity says it must always produce the same result! Remember that one of the benefits of pure functions is that you can substitute equal expressions, just like in algebra. So I ought to be able to replace:

[random(), random(), random()]

with something like

let x = random()
in [x,x,x]

But of course then we’d get the same number three times, rather than three different numbers.

What’s really going on inside the random number functions in imperative languages like Python, Java, or C? There is some internal state that needs to be referenced and then updated. The solution to doing this in Haskell involves making that internal state explicit, and passing it around as needed.

Here is a simple implementation of a pseudo-random number generator (PRNG) in Haskell.

data Seed = Seed { unSeed :: Integer }
  deriving (Eq, Show)

rand :: Seed -> (Integer, Seed)
rand (Seed s) = (s', Seed s')
  where
    s' = (s * 16807) `mod` 0x7FFFFFFF

We’re using a new type Seed, wrapped around an Integer, to represent the state of the generator. Then, the type of rand is:

Seed -> (Integer, Seed)

Compared to rand() or random() in imperative languages, the state transformation is explicit. This rand function takes a current state as an input, and returns the next state as an output, along with the generated pseudo-random number. Here’s an example of how to use it to generate multiple numbers. First you need to seed it with an initial state that we choose in some way, perhaps based on the current time of day or some “entropy pool” maintained by the machine on which we’re running. For these examples, I’ll just mash on the number row of my keyboard to generate initial seeds.

ghci> s0 = Seed 20924
ghci> rand s0
(351669668,Seed {unSeed = 351669668})

So starting with the seed 20924, our PRNG produced 351669668, and the new state is also 351669668. Never mind that the state and the generated number are the same – that’s just one of the quirks of this simple type of PRNG. Others algorithms use states that are hard to deduce from the generated numbers.

Because rand is a pure function, if we pass the same seed, we get the same result. But the way we’re supposed to use it is to take the seed returned by one call, and use it in the next call, like this:

ghci> s0 = Seed 982734
ghci> (r0,s1) = rand s0
ghci> (r1,s2) = rand s1
ghci> (r2,s3) = rand s2
ghci> [r0,r1,r2]
[1484424809,1410237664,87406909]

Unfortunately, it’s easy to make a mistake and reuse a previous state. That leads to repeating the same number!

ghci> s0 = Seed 287261
ghci> (r0,s1) = rand s0
ghci> (r1,s2) = rand s1
ghci> (r2,s3) = rand s1     -- Mistake! Should pass s2
ghci> [r0,r1,r2]
[533028333,1452901094,1452901094]  -- Duplicates

Let’s encapsulate generating three numbers into a function, so we can get it correct in one place, and then just call the function:

threeRandoms :: Seed -> ([Integer], Seed)
threeRandoms s0 = ([r0,r1,r2], s3)
  where (r0, s1) = rand s0
        (r1, s2) = rand s1
        (r2, s3) = rand s2

ghci> threeRandoms (Seed 3453)
([58034571,429459059,225867046],Seed {unSeed = 225867046})

If we want six random numbers, we could call threeRandoms twice, and compose the results:

sixRandoms :: Seed -> ([Integer], Seed)
sixRandoms s0 = (xs ++ ys, s2)
  where (xs, s1) = threeRandoms s0
        (ys, s2) = threeRandoms s1

So again, we thread the state through the two calls to threeRandoms. This is a pattern we’ll see over and over, because it applies to lots of different problems – not just generating random numbers. Eventually we’ll learn some notation that makes it a little more direct and less error-prone, but behind the scenes we’re still passing around the state like this.

ghci> sixRandoms (Seed 282)
([4739574,201125279,173303775,728721093,516171210,1603076237],Seed {unSeed = 1603076237})

For convenience, instead of generating a constant number of randoms at a time, we could just generate an infinite list of them. Interestingly, this one can’t have the same type as usual state-passing functions – state -> (result, state) – because we may need to use the state infinitely many times, so there is no final state we can return. So it just takes the Seed and continues to use it as long as needed.

allRandoms :: Seed -> [Integer]
allRandoms s0 = r0 : allRandoms s1
  where (r0, s1) = rand s0

ghci> take 10 $ allRandoms (Seed 211)
[3546277,1620219070,929265530,1664681726,888815766,
 430330630,1989458961,516373737,711980232,472878140]

We can map over the infinite random stream to produce models of coin flips (True for heads, False for tails) or dice rolls (integers in range [1..6]).

coinFlips :: Seed -> [Bool]
coinFlips s0 = map even $ allRandoms s0

diceRolls :: Seed -> [Integer]
diceRolls = map (succ . (`mod` 6)) . allRandoms

ghci> take 10 $ diceRolls (Seed 202)
[5,3,1,1,6,1,4,4,4,3]
ghci> take 10 $ coinFlips (Seed 202)
[True,True,True,True,False,True,False,False,False,True]

To test the quality of our PRNG, we can see whether, over the long run, we get the expected number of results for coin flips or dice rolls. For example, with \(n\) coin flips, we expect \(\frac{n}{2}\) heads:

countHeads n = length $ filter id $ take n $ coinFlips (Seed 299)

ghci> countHeads 10
6
ghci> countHeads 100
47
ghci> countHeads 1000
501
ghci> countHeads 10000
5002
ghci> countHeads 100000
50042

That’s really good; we’re getting pretty close to 50%. For coin flips, let’s count how many times we roll a one. It should be one in six, which is \(\frac{1}{6} = 0.1666\dots\)

countSnakeEye n = length $ filter (==1) $ take n $ diceRolls (Seed 299)

ghci> countSnakeEye 100
13
ghci> countSnakeEye 1000
162
ghci> countSnakeEye 10000
1659
ghci> countSnakeEye 100000
16582
ghci> countSnakeEye 1000000
166880

Traversals

We’ve seen how to thread the PRNG state through functions like threeRandoms and sixRandoms, so now let’s try a more sophisticated example: passing around the state as we traverse a tree in a particular order.

We’ll reuse the same tree data type as before, where the Leaf is just an empty placeholder, and the Branch carries a value as well as a left and right sub-tree.

data Tree a
  = Leaf
  | Branch { value :: a, left, right :: Tree a }
  deriving (Show)

And here’s a sample tree we used before:

sample1 :: Tree String
sample1 =
  Branch "A"
    (Branch "K"
       (Branch "M"
          Leaf
          (Branch "Q" Leaf Leaf))
       (Branch "P" Leaf Leaf))
    Leaf

I’ll also include the pretty-printing code at the bottom of this file, so we can do this:

ghci> printTree sample1
- "A"
  |- "K"
  |  |- "M"
  |  |  |- *
  |  |  |- "Q"
  |  |- "P"
  |- *

The first thing we’ll try is to keep the same tree shape but substitute each value with a pseudo-random integer. The figure shows how a pre-order traversal on this tree would operate, visiting each node before its left and then right subtrees.

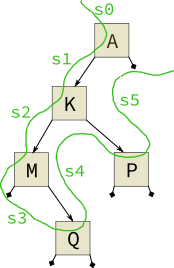
Threading state around a pre-order traversal

The labels on the curvy green line show subsequent states produced each time rand is called. The implementation of preorderRand is below:

preorderRand :: Tree a -> Seed -> (Tree Integer, Seed)
preorderRand Leaf s0 = (Leaf, s0)
preorderRand (Branch _ left right) s0 =
  (Branch newValue newLeft newRight, s3)
  where (newValue, s1) = rand s0
        (newLeft, s2) = preorderRand left s1
        (newRight, s3) = preorderRand right s2

Notice that its type includes the usual signature of a state-passing function: state -> (result, state). In this case the initial tree has type Tree a because we don’t care what values it stores; we’ll just be replacing them. The resulting type is Tree Integer.

Notice also the usual state-threading, how we’re given s0, and pass that to rand, producing s1. Then we give s1 to preorderRand left, producing s2. Then we use s2 in preorderRand right, producing s3.

Here are a couple of trees in the shape of sample1 but with random values:

ghci> (t0, s1) = preorderRand sample1 (Seed 2924)
ghci> printTree t0
- 49143668
  |- 1323907628
  |  |- 837437229
  |  |  |- *
  |  |  |- 199685365
  |  |- 1742472941
  |- *

ghci> (t1, s2) = preorderRand sample1 s1
ghci> printTree t1
- 508225248
  |- 1199279017
  |  |- 927977
  |  |  |- *
  |  |  |- 564123910
  |  |- 90253865
  |- *

Generalizing

Threading state isn’t just for random numbers; we actually can express many other computations this way. So instead of hard-coding rand into it, let’s take the state-transformation function as an extra parameter, called gen in this definition:

preorderState :: (a -> s -> (b,s)) -> Tree a -> s -> (Tree b, s)
preorderState gen Leaf s0 = (Leaf, s0)
preorderState gen (Branch value left right) s0 =
  (Branch newValue newLeft newRight, s3)
  where (newValue, s1) = gen value s0
        (newLeft, s2) = preorderState gen left s1
        (newRight, s3) = preorderState gen right s2

You can tell gen takes the role of a state transformer because its type includes s -> (b,s). Unlike when we used rand, we’ll also let it take the current value of the branch, so it can use that value to generate a new one. We can get back exactly the same preorderRand behavior by passing const rand:

ghci> (t0, s1) = preorderState (const rand) sample1 (Seed 2924)
ghci> printTree t0
- 49143668
  |- 1323907628
  |  |- 837437229
  |  |  |- *
  |  |  |- 199685365
  |  |- 1742472941
  |- *

It will also support other uses. Here’s one that keeps track of an integer counter, and pairs it with the value:

withCounter :: a -> Int -> ((a, Int), Int)
withCounter value n = ((value, n), n+1)

For the new state, it returns n+1 so that the next time it is called, the counter has been incremented.

ghci> (t0, _) = preorderState withCounter sample1 10
ghci> printTree t0
- ("A",10)
  |- ("K",11)
  |  |- ("M",12)
  |  |  |- *
  |  |  |- ("Q",13)
  |  |- ("P",14)
  |- *

Or this is kind of a neat idea: suppose we inject a new value into the root of the tree, and then rotate all the other values around and discard the last value.

inject :: a -> a -> (a, a)
inject value next = (next, value)

ghci> (t0, _) = preorderState inject sample1 "Z"
ghci> printTree t0
- "Z"
  |- "A"
  |  |- "K"
  |  |  |- *
  |  |  |- "M"
  |  |- "Q"
  |- *

We injected the new "Z" value into the root, moved "A" into the left child, "K" into the place of "M" and so on, and then discarded the final node, "P".

One nice thing about this generalization is that these state transformations can also be used with other data structures, such as lists. Here’s a function to thread state through the elements of a list:

threadList :: (a -> s -> (b,s)) -> [a] -> s -> ([b], s)
threadList gen [] s0 = ([], s0)
threadList gen (x:xs) s0 = (newHead : newTail, s2)
  where (newHead, s1) = gen x s0
        (newTail, s2) = threadList gen xs s1

And I’ll apply it with all the same examples as above:

ghci> threadList (const rand) "hello" (Seed 338)
([5680766,987353694,847394689,50991119,161761880],Seed {unSeed = 161761880})
ghci> threadList withCounter "hello" 5
([('h',5),('e',6),('l',7),('l',8),('o',9)],10)
ghci> threadList inject "hello" 's'
("shell",'o')

Admin

• Exam is next week, first hour of class.
• Written only, no computers, not writing code from scratch
• I’ll have practice problems available on Friday 20th.
• Assignment 6 deadline extended, but 1-2 questions added

Main program

I’m not using this for anything, but if you compile this with runghc, it requires a main, so here it is.

main = return ()

prettyPrint :: Show a => String -> Tree a -> String
prettyPrint indent Leaf = indent ++ "- *\n"
prettyPrint indent (Branch v Leaf Leaf) =
  indent ++ "- " ++ show v ++ "\n"
prettyPrint indent (Branch v l r) =
  indent ++ "- " ++ show v ++ "\n" ++ prettyPrint tab l ++ prettyPrint tab r
  where tab = indent ++ "  |"

printTree :: Show a => Tree a -> IO ()
printTree = putStrLn . prettyPrint ""