import Data.Monoid

Some follow-up from A5

To some degree, you can use types to guide the code. We call this “type-directed programming.” I’ll illustrate it with examples from the first part of assignment 5.

Suppose we already wrote the maybeCapitalize function – I’ll add it with an error placeholder here:

maybeCapitalize :: String -> String
maybeCapitalize = error "TODO"

Now we want write titleCase. We know it involves words, which splits strings into lists; and unwords, which joins them back together again. Here are their types:

words :: String -> [String]
unwords :: [String] -> String

We want to capitalize each word in the list, so really we’ll be using the capitalization with map, at this type:

map maybeCapitalize :: [String] -> [String]

But how to compose these pieces together? The diagram summarizes what we have, and the larger box at the bottom, labeled titleCase, shows how they should be composed. We can almost derive this entirely from the types – there just aren’t many choices for connecting these functions together such that the types of inputs and outputs match up correctly.

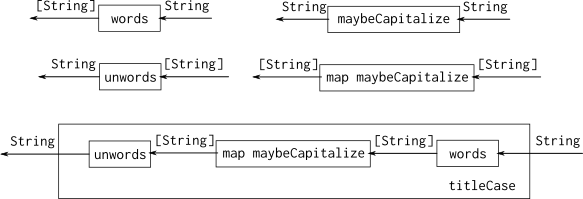
Composing titleCase from other functions

However, there are some variations in the syntax we use for this composition. In this first attempt, we use parentheses to indicate the ordering: apply words to the argument s first, then feed the result into map maybeCapitalize, then feed that into unwords:

titleCase1 :: String -> String
titleCase1 s = unwords (map maybeCapitalize (words s))

The function applications must be grouped to the right using parentheses. You’ve probably seen me use the $ operator before. It just represents function application, so f $ x is exactly the same as f x operationally; the only difference is in the precedence and associativity.

Normally when things are placed side-by-side in a function application, you associate to the left. So we interpret f x y z as though it were written (((f x) y) x). If you want it grouped to the right, as in titleCase1, then you can place the $ operator between the items: f $ x $ y $ z is interpreted as (f $ (x $ (y $ z))). So here we rewrite it using $ and we don’t need parentheses:

titleCase2 :: String -> String
titleCase2 s = unwords $ map maybeCapitalize $ words s

Another option is to use the function composition operator, parenthesize the entire composition, and then apply it as a whole to the argument:

titleCase3 :: String -> String
titleCase3 s = (unwords . map maybeCapitalize . words) s

Once you’ve got that, a lot of Haskell programmers would do a transformation known as “Eta reduction” (after the Greek letter $\eta$). This transformation will take a function of the form:

f x = (......something......) x

and – as long as x does not appear at all in the something section – we can eliminate the argument and just say that the function titleCase4 is the composition of these other functions directly:

titleCase4 :: String -> String
titleCase4 = unwords . map maybeCapitalize . words

Of course, this is not the completely correct version of titleCase from the assignment. This one uses maybeCapitalize on all the words, whereas the correct solution should unconditionally capitalize the first, and only use maybeCapitalize on the rest.

Monoid follow-up

A type is a monoid if it has an “empty” value, and an “append” function (aka <>), and they obey the following laws:

mempty <> x == x (left-identity law)
x <> mempty == x (right-identity law)
(x <> y) <> z == x <> (y <> z) (associative law)

So you can think of “monoid” as meaning “appendable”, but there are other legitimate ways to interpret these laws too.

Numeric monoids

These laws should look pretty familiar, because they’re the same laws we have for addition and multiplication over integers and real numbers. For addition, mempty would be the additive identity (zero). For multiplication, it would be the multiplicative identity (one).

Since there are at least these two ways to form monoids over numbers, we don’t automatically have instances of Monoid for Int and Float — it would be ambiguous whether you want the addition version or the multiplication version. However, Haskell does have a way to select them, using the constructors (and types) named Sum or Product:

ghci> mempty :: Sum Int          -- Produce the additive identity
Sum {getSum = 0}
ghci> mempty :: Sum Float
Sum {getSum = 0.0}
ghci> mempty :: Product Int      -- Multiplicative identity
Product {getProduct = 1}
ghci> mempty :: Product Float
Product {getProduct = 1.0}

You can then add and multiply using (<>), though it’s pretty awkward:

ghci> Sum 3 <> Sum 5                   -- Using monoid for 3+5
Sum {getSum = 8}
ghci> Product 3 <> Product 5           -- Using monoid for 3*5
Product {getProduct = 15}
ghci> mconcat $ map Sum [1..10]        -- Sum of list
Sum {getSum = 55}
ghci> mconcat $ map Product [1..10]    -- Product of list
Product {getProduct = 3628800}

Those last two examples use mconcat, which is a third method in the Monoid class. It has this type:

mconcat :: Monoid a => [a] -> a

and should obey these laws:

x <> y = mconcat [x,y]
mconcat [] == mempty
mconcat (h:t) == h <> mconcat t

So it just repeatedly applies mappend to whatever is in the list.

`Ordering` monoid

Haskell features a compare function in its Ord type class. The type of compare is:

compare :: Ord a => a -> a -> Ordering

where Ordering is defined as follows:

data Ordering = LT | EQ | GT

So it’s just an enumeration of these three tags, representing whether the values being compared are less-than, equal, or greater:

ghci> compare 3 5
LT
ghci> compare 3 3
EQ
ghci> compare 5 3
GT
ghci> compare "amy" "alice"
GT

Using compare and Ordering rather the usual comparison operators (<, >, <=, etc.) allows us to discriminate the three possibilities without an if-else chain. Consider these:

-- Version 1: if-else chain
if actual < expected then "Too small"
else if actual > expected then "Too big"
else "You got it!"

-- Version 2: Ordering and case
case compare actual expected of
  LT -> "Too small"
  GT -> "Too big"
  EQ -> "You got it!"

The interesting thing about Ordering for our present discussion is that it’s a monoid – although, interestingly, it doesn’t obey all the monoid laws! The empty value is EQ:

ghci> mempty :: Ordering
EQ

Then the append operation results in the left operand, unless it’s EQ – then it uses the right operand.

ghci> LT <> LT
LT
ghci> LT <> EQ
LT
ghci> LT <> GT
LT
ghci> GT <> LT
GT
ghci> GT <> EQ
GT
ghci> GT <> GT
GT
ghci> EQ <> LT
LT
ghci> EQ <> GT
GT
ghci> EQ <> EQ
EQ

The overall effect is that two comparisons can be merged, and the second is used to break a tie in the first. This is helpful for various kinds of lexicographic ordering. For example, we might have a type representing a person, which carries their first and last names, and date of birth:

data Person = Person { firstName, lastName :: String, birthDate :: Int }
   deriving (Show, Eq)

alice = Person "Alice" "Jones"    19881015
bob   = Person "Bob"   "Danforth" 19930324
chuck = Person "Chuck" "Jones"    19120921

So here is a comparison function that checks the last name, and moves on to the first only if the last names are EQ.

compareLastFirst p1 p2 =
  compare (lastName p1) (lastName p2) <>
  compare (firstName p1) (firstName p2)

ghci> compareLastFirst alice bob
GT
ghci> compareLastFirst alice chuck
LT
ghci> compareLastFirst alice alice
EQ

Or you can order by birth date, then names:

compareAge p1 p2 =
  compare (birthDate p1) (birthDate p2) <>
  compareLastFirst p1 p2

ghci> compareAge alice bob
LT
ghci> compareAge alice chuck
GT

If you’d like to install one of these as the default way to compare Person values, we can declare an instance of the Ord class:

instance Ord Person where
  compare = compareLastFirst

Now you have < and <= and other comparison operators that work too:

ghci> alice < bob
False
ghci> alice < chuck
True
ghci> chuck >= chuck
True

`BoundedStack` monoid

Finally, let’s revisit the BoundedStack monoid from the assignment. I’ll repeat the essential definitions:

data BoundedStack a
  = BoundedStack { capacity :: Int, elements :: [a] }
  deriving (Show, Eq)

new :: Int -> BoundedStack a
new n = BoundedStack { capacity = n, elements = [] }

push :: a -> BoundedStack a -> Maybe (BoundedStack a)
push elem (BoundedStack cap elems)
  | cap > 0 = Just $ BoundedStack (cap-1) (elem:elems)
  | otherwise = Nothing

and now here’s the instance:

instance Monoid (BoundedStack a) where
  mempty = new 0
  mappend (BoundedStack cap1 elems1) (BoundedStack cap2 elems2) =
    BoundedStack (cap1+cap2) (mappend elems1 elems2)

The capacity of the merged stack is the sum of the capacities of the original ones, and the elements are likewise appended.

There seems to be some discretion in the definition of mempty – sure it should return an empty stack, but what should the capacity be? Does it need to be zero?

Zero is a good choice because it’s the only one that will obey the monoid identity laws. Otherwise, if mempty is defined to be, say, new 5 – you end up with this:

ghci> Just s1 = push 7 (new 3)
ghci> s1
BoundedStack {capacity = 2, elemetns = [7]}
ghci> s1 <> mempty
BoundedStack {capacity = 7, elements = [7]}

This is technically a violation because s1 <> mempty does not equal s1. (Even so, you could get away with this definition for most purposes, if you prefer it for some reason.)

Explanation of type classes

We’ve been using type classes such as Monoid, Functor, Eq, Ord, and Show. Basically, a type class defines a set of consistent operations over specified types, which are called instances of the class. This is an effective way to handle “overloading” – the same function name can be defined differently on different types.

Here’s an example where we define types representing different two-dimensional geometric shapes (Circle, Rectangle), and then a function area that’s defined differently for different shapes.

data Circle = Circle { centerX, centerY, radius :: Float }
  deriving Show

data Rectangle = Rectangle { x1, y1, x2, y2 :: Float }
  deriving Show

These are two completely distinct types, but we can define a common interface over their values:

class Shape a where
  area :: a -> Float
  bump :: a -> a

The area function should take a value of an instance of Shape, and calculate its area, returning a single floating-point number. The bump function will move the shape within the coordinate system by offseting its coordinates by $+1$ in both dimensions.

Now here are the instances for our two shapes:

instance Shape Circle where
  area (Circle x y r) = pi * r * r
  bump (Circle x y r) = Circle (x+1) (y+1) r

instance Shape Rectangle where
  area (Rectangle x1 y1 x2 y2) = abs (x1 - x2) * abs (y1 - y2)
  bump (Rectangle x1 y1 x2 y2) = Rectangle (x1+1) (y1+1) (x2+1) (y2+1)

Laziness

In many programming languages, the arguments of functions are strict – meaning that the arguments are fully evaluated before the function is called. So f(x/0) will crash with a division by zero no matter how f is defined – we don’t even get a chance to run f.

However, in these strict languages, there are parts of the code that can be excluded from evaluation, based on specified conditions. The simplest example is an if-then-else:

if 3 < 5 then 42 else 9/0

This code would never get to the division by zero, because the condition is true. The other place you see this is the Boolean and/or operators. They are called “short-circuit” operators.

3 < 1 && ........

Since the left side of the && is false, the right side doesn’t matter. Whatever its value is, the result of the entire compound expression will be false.

Similarly with a Boolean or, except that it’s short-circuited if the left side is true:

1 < 3 || .......

So in mainstream languages, these short-circuit operations can guard against errors:

x != 0 && 100/x > 5

There’s no way for this to do division by zero. If x were zero, then the left side would be false and the right side would be skipped.

Okay, so that’s the situation in many languages, where strictness is the default. But Haskell is the opposite! It’s non-strict by default. So we say that it’s lazy – it only ever evaluates something when you really need to see the result!

Here’s a demonstration. Suppose we generate a range of numbers that includes zero:

ghci> range = [-5..5] :: [Int]

Then we map a function that will divide by each element of the list:

ghci> map (100 `div`) range
[-20,-25,-34,-50,-100,*** Exception: divide by zero

Oops! It works for a while, but crashes when it gets to the zero. But if we only look at specific elements that don’t crash – even if they come after the bad one – it’s no problem:

ghci> take 3 results
[-20,-25,-34]
ghci> results !! 4
-100
ghci> results !! 6
100
ghci> last results
20

(The !! operator looks up the list element at the given location.)

GHCI has a built-in tool called sprint for examining a value without forcing further evaluation:

ghci> :sprint results
results = [-20,-25,-34,_,-100,_,100,_,_,_,20]

The underscores _ indicate elements that haven’t been demanded yet, so they have not been computed. We just have the first three (due to take 3), the ones at indices 4 and 6 (due to !!), and the last one (due to last).

‘Infinite’ data structures

Laziness has lots of uses, and a few pitfalls. One interesting use we’ll explore for now is that it enables (potentially) infinite data structures. Of course, you can’t really represent an infinite data structure in finite memory. But we can describe the infinite data structure (often recursively), and then only the parts we actually need are calculated and kept.

A simple example is that we can define a name which represents all of the natural numbers:

ghci> nats = [0..]

We used the .. range notation to construct a list, but there is no endpoint. So the list potentially can go on forever. You can ask for the first three, or for any particular element:

ghci> take 3 nats
[0,1,2]
ghci> nats !! 245
245

But if you make the mistake of asking for the length of the list… it will produce an infinite loop, so your GHCI process will use up more and more of your computer’s memory and everything else will get sluggish. Eventually it will have to be killed, either by your OS when it truly eats up all the memory, or by you hitting Control-C.

ghci> length nats

[Ctrl-C]
Interrupted.

Here’s a really classic, clever use of an infinite data structure to compute the Fibonacci sequence. This is the sequence that starts with 1,1 (or 0,1) and the next number is always the sum of the previous two: 1, 1, 2, 3, 5, 8, 13, 21…

fibs :: [Integer]
fibs = 1 : 1 : zipWith (+) fibs (tail fibs)

This definition is twice-recursive. The zipWith (+) means you’re lining up fibs with its own tail, and then adding to produce subsequent entries in the list. The first two entries are (and must be) given.

Again, it’s a potentially infinite list, so don’t make the mistake of printing the whole thing or asking its length. But otherwise you can use it pretty normally. Here are the first 10 numbers:

ghci> take 10 fibs
[1,1,2,3,5,8,13,21,34,55]

Here is the 100th:

ghci> fibs !! 100
573147844013817084101

One of the interesting properties of the Fibonacci sequence is that the ratio of consecutive numbers approaches the irrational number $\phi$, also known as the golden ratio. So here’s a way to generate different approximations of the golden ratio:

golden n = fromIntegral (fibs !! (n+1)) / fromIntegral (fibs !! n)

The larger n you provide, the closer the result is to $\phi$:

ghci> golden 5
1.625
ghci> golden 10
1.6179775280898876
ghci> golden 20
1.618033985017358
ghci> golden 30
1.6180339887496482
ghci> golden 40
1.618033988749895

Threading state through recursion

I did not explain this very well. We’ll visit it again next class.

data Tree a
  = Leaf
  | Branch { value :: a, left, right :: Tree a }
  deriving (Show)

sample1 :: Tree String
sample1 =
  Branch "A"
    (Branch "K"
       (Branch "M"
          Leaf
          (Branch "Q" Leaf Leaf))
       (Branch "P" Leaf Leaf))
    Leaf

sample2 :: Tree String
sample2 =
  Branch "B"
    (Branch "S"
       Leaf
       (Branch "C"
          (Branch "D" Leaf Leaf)
          (Branch "F" Leaf Leaf)))
    (Branch "R" Leaf Leaf)

numberNodesInOrder :: Int -> Tree a -> (Tree (a, Int), Int)
numberNodesInOrder next Leaf = (Leaf, next)
numberNodesInOrder next (Branch value left right) =
  (Branch (value, middleNum) newLeft newRight, lastNum)
  where (newLeft, middleNum)  = numberNodesInOrder next left
        (newRight, lastNum) = numberNodesInOrder (middleNum+1) right

Main program

I’m not using this for anything, but if you compile this with runghc, it requires a main, so here it is.

main = return ()

PDF

Source

Notes from 10/12