One complaint about statically typed languages like C++ and Java is that specifying the types of every variable and parameter can be tedious and repetitive. Nowhere is this more obvious than in Java:

ANTLRInputStream input = new ANTLRInputStream("a=3");
HashMap<String,Object> model = new HashMap<String,Object>();

It seems that we’re often specifying the type twice: on the left to declare the type of the variable, and on the right to invoke the constructor for that class.

In revision 8 of the Java language, the compiler gained the ability to infer type parameters from the context, but we still need to specify them in the variable declaration:

HashMap<String,Object> model = new HashMap<>(); // infers within 'diamond' <>

so it’s a very limited and obvious form of inference. In these notes we’ll explore a much more sophisticated type system and inference technique.

Hindley-Milner type system

One of the best-explored and most elegant types systems that supports decidable inference is known as Hindley-Milner or sometimes Damas-Milner or some other combination of those names — after Roger Hindley, Robin Milner, and Luis Damas who each contributed (or rediscovered) various aspects of the system. It was developed for the ML programming language designed by Milner and others at the University of Edinburgh in the early 1970s. Variations of the Hindley-Milner system are used today in the ML family (Standard ML, OCaml) and related functional languages such as Haskell, Scala, F#, and Swift.

In HM type systems every variable, function, and expression has a statically-determined principal type, but the programmer never (or almost never) needs to specify types in the code.

One downside of HM is that it’s generally not compatible with automatic promotions (like the int→float in C/C++/Java) or subtyping (as used in object-oriented class hierarchies). With extensions to HM, these features can be partly supported, but they always involve compromise.

This is why the ML family of languages treat different numeric types as completely distinct, requiring any conversion between them to be explicit. In OCaml, the usual arithmetic operators (+ - * /) work only on int values, but there are a separate set of operators distinguished by a dot character for float values (+. -. *. /.). Mixing them up produces type errors:

# 3 + 4 ;;
- : int = 7
# 3.1 +. 4.0 ;;
- : float = 7.1
# 3.1 + 4.0 ;;
Error: This expression has type float but an expression was expected of type int
# 3.1 +. 4 ;;
Error: This expression has type int but an expression was expected of type float

(The pound sign at the beginning of each line is the OCaml prompt.)

In Standard ML, the floating-point type is called real and you also can’t mix it with int, although the standard numeric operators (+ - * /) are overloaded to support both types:

- 3 + 4;
val it = 7 : int
- 3.2 + 4.0;
val it = 7.2 : real
- 3.2 + 4;
stdIn:38.1-38.8 Error: operator and operand don't agree [overload conflict]
  operator domain: real * real
  operand:         real * [int ty]
  in expression:
    3.2 + 4
- real;
val it = fn : int -> real
- 3.2 + real 4;
val it = 7.2 : real

(The dash on the beginning of each line is the SML prompt.)

Parametric polymorphism

In object-oriented programming, polymorphism refers to the ability to provide the same interface to different underlying structures. So if you have a collection of Mammal objects, it could actually contain an Elephant, a Mouse, and a Dolphin object (where those are subclasses of Mammal) but you work with them using the interface of Mammal, the base class.

The HM type system supports a different form of polymorphism known as parametric polymorphism. This is essentially the “for-all” (\(\forall\)) operator in mathematical logic. The for-all binds a type variable that can later be instantiated with an actual type. Consider the type written as \(\forall\alpha.\;\alpha\!\to\!\alpha\). This is the type of a polymorphic function that takes a parameter of some type (represented by the variable \(\alpha\) “alpha”) and returns a value of the same type. When I apply that function to an integer value, I get back an integer. In that case, we instantiate the type by setting \(\alpha\!=\!\texttt{int}\) and the result is \(\texttt{int}\!\to\!\texttt{int}\). But the function can also be applied to a string, in which case we’d get back a string. Setting \(\alpha\!=\!\texttt{string}\) instantiates the type to \(\texttt{string}\!\to\!\texttt{string}\).

In SML syntax, type variables are distinguished from regular variables by starting them with a quote/apostrophe character: 'a, 'b, and so on. In practice, these are sometimes pronounced using the names of Greek letters like alpha, beta, gamma, since that’s how they appear in research papers that stylize types into a more mathematical notation, for example:

ASCII representation in SML: 'a * 'a list -> 'a list
Mathematical representation in research paper: \(\forall\alpha.\;\alpha\times\alpha\,\mathtt{list}\to\alpha\,\mathtt{list}\)
Typical pronunciation: “alpha cross alpha list to alpha list”

In SML, the for-all quantifier is only applied at the top level (all the way to the left), to bind any variables used in the type. SML doesn’t support nested uses of \(\forall\), although some related languages do. Because the quantifier is always at the top level, we can omit it in SML type notation — it’s implicit.

Incidentally, the cross operator represents a pair of values. It has higher precedence than the arrow, and the application of the variable to the list operator in \(\alpha\,\mathtt{list}\) is even higher. So this type is grouped as:

\[(\alpha\times(\alpha\,\mathtt{list}))\to(\alpha\,\mathtt{list})\]

rather than \(\alpha\,\times\,(\alpha\,\mathtt{list}\!\to\!\alpha\,\mathtt{list})\) or \((\alpha\!\times\!\alpha)\,\mathtt{list}\to\alpha\,\mathtt{list}\).

Here is a grammar for a slightly-simplified language of SML types, and a parse tree representation of a sample type.

typ : VAR                           # TypeVar
    | typ longid                    # TypeApp
    | longid                        # TypeId
    | '(' typ ')'                   # TypeParen
    | type '*' type                 # TypePair
    | <assoc=right> typ '->' typ    # TypeArrow
    ;

longid : (ID '.')* ID;

ID  : [A-Za-z] [A-Za-z0-9_]* ;
VAR : '\'' [A-Za-z0-9_]+ ;

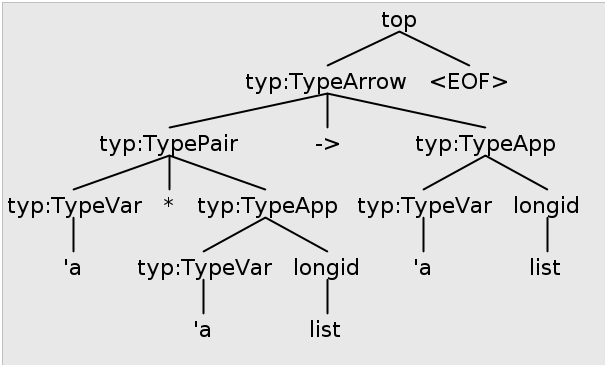
Parse tree for 'a * 'a list -> 'a list

Instantiation and substitution

One of the operations we often need to apply to types is to replace one of the type variables with a new type. This is called instantiation. We already saw an example of it above: start with \(\forall\alpha.\;\alpha\!\to\!\alpha\), then set \(\alpha\!=\!\texttt{int}\), and the result is \(\texttt{int}\!\to\!\texttt{int}\).

The only possible complication to instantiation is when the type being substituted also contains type variables. For example, let’s start with \(\forall\alpha,\beta.\; \alpha\times\beta\to\alpha\), and suppose we want to instantiate \(\beta=\forall\alpha.\;\alpha\,\mathtt{list}\to\mathtt{int}\). A naive replacement might be \(\forall\alpha.\; \alpha\times(\alpha\,\mathtt{list}\to\mathtt{int})\to\alpha\), but the problem with that is we mixed up two different variables because both are named \(\alpha\). The \(\alpha\) in one type crossed into the scope of the \(\alpha\) in the other type.

To resolve this problem, we can always rename bound variables before instantiating, so that no variable names conflict. This renaming is known formally as “\(\alpha\)-conversion”, and two types that are equivalent except for the names of bound variables are “\(\alpha\)-equivalent.”

So in the problem above, before substituting \(\beta=\forall\alpha.\;\alpha\,\mathtt{list}\to\mathtt{int}\), we can rename the \(\alpha\) (bound by the for-all) to some other distinct name, for example \(\delta\) “delta”:

In the type \(\forall\alpha,\beta.\; \alpha\times\beta\to\alpha\)
We want to substitute \(\beta=\forall\alpha.\;\alpha\,\mathtt{list}\to\mathtt{int}\)
The variable names conflict, so rename \(\alpha\) to \(\delta\) in \(\beta=\forall\delta.\;\delta\,\mathtt{list}\to\mathtt{int}\)
And then apply the substitution, producing \(\forall\alpha,\delta.\; \alpha\times(\delta\,\mathtt{list}\to\mathtt{int})\to\alpha\)

Notice that when instantiating with a type that itself contains a for-all, we lift the for-all to the top (all the way to the left) rather than nesting it. Otherwise, the result would be \(\forall\alpha.\; \alpha\times(\forall\delta.\;\delta\,\mathtt{list}\to\mathtt{int})\to\alpha\), which is not allowed in SML.

A set of variable replacements such as these is known as a substitution. It’s common to instantiate several variables at once. For example here are two different substitutions, each with two or more variables being instantiated:

\(s_1 = \{\alpha=\mathtt{int}, \beta=\mathtt{string}\}\)
\(s_2 = \{\alpha=\mathtt{string}, \beta=\forall\delta.\delta\to\mathtt{string}, \gamma=\mathtt{real}\}\)

Suppose we have the type:

\(T = \forall\alpha,\beta,\gamma.\; \alpha\to\beta\to\gamma\to \alpha\times\beta\times\gamma\)

We can apply different substitutions to the same type:

\(s_1(T) = \forall\gamma.\; \mathtt{int}\to\mathtt{string}\to\gamma\to \mathtt{int}\times\mathtt{string}\times\gamma\)
\(s_2(T) = \forall\delta.\; \mathtt{string}\to(\delta\to\mathtt{string})\to\mathtt{real}\to \mathtt{string}\times(\delta\to\mathtt{string})\times\mathtt{real}\)

Again, in applying the substitution \(s_2\) to \(T\), we lifted the \(\forall\delta\) to the top level.

Type unification

Hindley-Milner type inference is based primarily on an operation called unification. This is a way of making two types equivalent by coming up with a substitution to apply to both. For example, let’s consider these two types:

\(T_1 = \forall\alpha.\; \alpha\times\mathtt{int}\to\alpha\)
\(T_2 = \forall\beta,\gamma.\; \mathtt{string}\times\beta\to\gamma\)

We have intentionally made all the bound variable names distinct. If they don’t start out that way, we can always achieve it by renaming (\(\alpha\)-conversion). Unifying \(T_1\) and \(T_2\) produces this substitution:

\(s_3 = \{\alpha=\mathtt{string}, \beta=\mathtt{int}, \gamma=\mathtt{string}\}\)

which when applied to each type:

\(s_3(T_1) = \mathtt{string}\times\mathtt{int}\to\mathtt{string}\)
\(s_3(T_2) = \mathtt{string}\times\mathtt{int}\to\mathtt{string}\)

produces equivalent types (actually, \(\alpha\)-equivalent types, if they still contain bound variables).

When two types are supposed to be compatible but cannot be unified, the compiler reports it as a type mismatch. Unification takes the place of simpler calculations like the Least Upper Bound (LUB) we used in the calculator language.

Now we’ll describe the unification algorithm. Start by ensuring that all bound type variables are distinct. The algorithm proceeds recursively by cases that depend on the two types being unified. At each stage, the unification can succeed or fail, and as it progresses it builds up a substitution of variables. In order to \(\textbf{Unify}(\tau_1, \tau_2)\):

If both types are IDs (TypeID in the grammar), then those IDs must be exactly the same, or else unification fails.
If both types are the same type variable, unification succeeds with no substitution of variables.
If the left type \(\tau_1\) is a variable such as \(\alpha\), and that variable does not appear free in the right type \(\tau_2\), then add \(\alpha=\tau_2\) to the substitution and unification succeeds.
(This rule is symmetric with the previous one.) If the right type \(\tau_2\) is a variable such as \(\alpha\), and that variable does not appear free in the left type \(\tau_1\), then add \(\alpha=\tau_1\) to the substitution and unification succeeds.
If both types are an application of a type to an ID (TypeApp in the grammar), then the IDs must be the same and the types being applied must unify. That is, \(\textbf{Unify}(\tau_3\;\mathtt{ID}, \tau_4\;\mathtt{ID})\) succeeds if and only if, recursively, \(\textbf{Unify}(\tau_3, \tau_4)\) succeeds.
If both types represent pairs using the cross \(\times\) (or multiplication *) operator, then we first try to unify the left sides of each pair. If that succeeds, we apply the resulting substitution to the right sides of each pair, and unify them.
(This rule is the same pattern as the previous rule.) If both types represent functions using the arrow \(\to\) (->) operator, then we first try to unify the argument types of each function. If that succeeds, we apply the resulting substitution to the result types of each function, and unify them.
Finally, if none of the above cases apply, unification fails.

Let’s work through a few examples in detail, following the algorithm. Beginning with these examples, we’ll allow \(t_1\dots t_n\) to represent distinct type variables, rather than having to come up with more Greek letters.

Unification example 1

\(T_1 = t_1\times t_2 \;\to\; t_2\)
\(T_2 = t_3 \to \mathtt{int} \to t_4\)

It can help to fully parenthesize these types, so it’s easier to see the structure:

\(T_1 = (t_1\times t_2) \;\to\; t_2\)
\(T_2 = t_3 \to (\mathtt{int} \to t_4)\)

Equivalently, we can draw the parse trees.

Parse trees for 't1 * 't2 -> t2 and 't3 -> int -> 't4, for unification example 1.

\(\textbf{Unify}(T_1, T_2)\): At the top level (the root of the parse trees), both \(T_1\) and \(T_2\) are arrow types, so they match rule 7. We try to unify the left sides.
- \(\textbf{Unify}(t_1\times t_2, t_3)\): Here, the right type is just a variable, so this matches rule 4. We add \(\{t_3 = t_1\times t_2\}\) to the substitution, and this unification succeeds.
- \(\textbf{Unify}(t_2, \mathtt{int}\to t_4)\): Now the left type is just a variable, so this matches rule 3. We add \(\{t_2 = \mathtt{int}\to t_4\}\) to the substitution, and unification succeeds.
So now we’re done. The unification of \(T_1\) and \(T_2\) succeeds with the substitution \(s = \{t_3 = t_1\times t_2,\;\; t_2 = \mathtt{int}\to t_4\}\). Applying this to either of the original types produces \(s(T_1) = s(T_2) = (t_1\times (\mathtt{int}\to t_4)) \;\to\; (\mathtt{int}\to t_4)\).

Unification example 2

Again, let’s start with fully-parenthesized types, with distinctly-named variables.

\(T_1 = t_1 \;\to\; (t_2\times (t_1\;\mathtt{list}))\)
\(T_2 = \mathtt{int} \;\to\; (t_3\times (\mathtt{real}\;\mathtt{list}))\)
\(\textbf{Unify}(T_1, T_2)\): At the top level both \(T_1\) and \(T_2\) are arrow types, so they match rule 7. We try to unify the left sides.
- \(\textbf{Unify}(t_1, \mathtt{int})\): Here, the left type is just a variable, so this matches rule 3. We add \(\{t_1=\mathtt{int}\}\) to the substitution, and unification succeeds.
- \(\textbf{Unify}(t_2\times(t_1\;\mathtt{list}),\; t_3\times(\mathtt{real}\; \mathtt{list}))\): Now we try to unify the right sides, but first we apply the substitution generated so far, to eliminate the variable \(t_1\).
- \(\textbf{Unify}(t_2\times(\mathtt{int}\;\mathtt{list}),\; t_3\times(\mathtt{real}\; \mathtt{list}))\): At the top level, both of these are cross types (pairs), so they match rule 6. We try to unify the left sides.
  - \(\textbf{Unify}(t_2, t_3)\): Both are type variables, but they’re not the same. So we can apply either rule 3 or rule 4. Let’s apply rule 3 and add \(\{t_2 = t_3\}\) to the substitution.
  - \(\textbf{Unify}(\mathtt{int}\;\mathtt{list},\; \mathtt{real}\;\mathtt{list})\): These are type applications, rule 5. The IDs on the right must match, both are list. So then we unify the types on the left.
    - \(\textbf{Unify}(\mathtt{int},\; \mathtt{real})\): Uh-oh! These are both just IDs, rule 1. That rule says the IDs must be exactly the same. They are not, so unification fails.

Unification exercises

\(\textbf{Unify}(\mathtt{real}\to t_4,\;\; t_5\to(\mathtt{string}\to\mathtt{int}))\)
\(\textbf{Unify}(t_1\to(t_2\to\mathtt{real}),\;\; \mathtt{int}\to((t_3\;\mathtt{list})\to \mathtt{real}))\)
\(\textbf{Unify}((\mathtt{int}\;\mathtt{list})\;\mathtt{list},\;\; t_6\;\mathtt{list})\)
\(\textbf{Unify}(((t_7\;\mathtt{list})\times t_8)\times t_8, \;\; (t_9\times(t_{10}\;\mathtt{list}))\times t_9)\)

Heterogeneous AST for ML types

In this section, we present a class hierarchy used to represent abstract syntax trees for ML types. The base class TypeAST is abstract, so it only defines operations that are available on all of its subclasses. It also is used as the type of a variable referencing AST node when it can be any of the sub-classes. For example, the left and right components of a pair (the cross ‘\(\times\)’ operator) can themselves be type variables, or IDs, or arrow types, or other pairs. Therefore, the left and right fields are declared as being references to TypeAST, the base class of all of those.

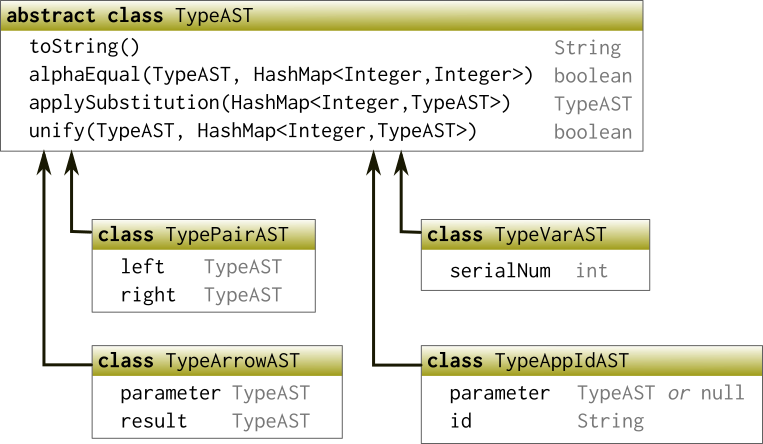
Class hierarchy representing abstract syntax trees for ML types

Each sub-class in the hierarchy has a constructor that takes references to its children. Here is some code using those constructors to create a representation of \((\alpha\;\mathtt{list}\times\mathtt{int}) \to \alpha\), or in ASCII SML notation: 'a list * int -> 'a:

    TypeAST alphaTy = new TypeVarAST();
    TypeAST alphaListTy = new TypeAppIdAST(alpha, "list");
    TypeAST intTy = new TypeAppIdAST("int");
    TypeAST pairTy = new TypePairAST(alphaListTy, intTy);
    TypeAST arrowTy = new TypeArrowAST(pairTy, alphaTy);

Basically, we build the abstract syntax tree bottom-up. The last variable defined, arrowTy, is the root node of this representation.

It’s worth understanding how type variables are represented, using TypeVarAST. We do not keep track of the type variable name in the source, whether it is 'a or 'b or `element. Instead, type variables are represented as integers. Each time we call the TypeVarAST constructor, it determines a new integer that has not been used previously, based on a static counter. So if these are the first three variables created in the program:

    TypeAST ta = new TypeVarAST(); // ta.serialNum == 1
    TypeAST tb = new TypeVarAST(); // ta.serialNum == 2
    TypeAST tc = new TypeVarAST(); // ta.serialNum == 3

they will get distinct serial numbers 1, 2, and then 3. This is a simple way to ensure that type variable names are distinct and to minimize the amount of variable renaming we need to do during substitution and unification.

It also means, however, that if we construct the same type twice, those representations will not be exactly the same.

    TypeAST tx = buildSampleType(); // 't4 * int -> 't4
    TypeAST ty = buildSampleType(); // 't5 * int -> 't5

The are, however, \(\alpha\)-equivalent. We will make use of a method alphaEqual to determine whether two types are equivalent. That process needs access to a map data structure it will use to keep track of matching type variable names. In this example:

    tx.alphaEqual(ty, new HashMap<Integer, Integer>());

the call to alphaEqual returns true, and afterwards the map would show that the serial number 4 is mapped to 5.

The other crucial methods we define on the TypeAST hierarchy are:

applySubstitution — this takes a map from integers to type nodes. It traverses the AST, producing a new AST which is the same except that type variables whose serial numbers are in the map are replaced with the corresponding node in the map. (In this method, the map parameter is read-only, it is not modified as it would be in alphaEqual and unify.)
unify — this method implements the unification algorithm described in the previous section. It returns a boolean value to indicate whether unification succeeds or failed. Also, it populates the given map with the substitutions that were generated by the algorithm.

Inferring ML function types

Here is a simple function definition in SML:

fun alice xs = if null xs then 0 else hd xs

The name of the function is alice, and it has a parameter named xs. (ML doesn’t use parentheses to distinguish function parameters; instead the function and its parameter are just placed side by side.)

The body of the function is to the right of the equal sign. It’s an if-then-else expression, and itself contains calls to two built-in functions, with these types:

null: 't1 list -> bool: tests whether the list is empty
hd: 't2 list -> 't2: returns the first element of the list

Although neither the type of the alice function nor of its parameter xs are mentioned in the code above, they do have well-defined types and the compiler is able to verify that the function type-checks. Here’s how it works.

From the fun keyword, we know that alice will be a function. Therefore it will have an arrow type. For now, let’s just fill in some arbitrary type variables for the parameter and result type. So we are positing that:

alice: \(t_3\to t_4\)
xs: \(t_3\)

Now we look at the body of the expression. It’s an if-then-else. This construct requires that the first expression unifies with boolean, and that the types of the ‘then’ and ‘else’ expressions unify.

The ‘if’ expression is null xs. Therefore the type of xs, \(t_3\) must unify with the parameter type of null, which is \(t_1\,\mathtt{list}\). According to rule 3 in our unification algorithm, we add the substitution \(\{t_3 \;=\; t_1\, \mathtt{list}\}\). Applying that substitution to the facts we know so far:

alice: \(t_1\,\mathtt{list}\to t_4\)
xs: \(t_1\,\mathtt{list}\)

The return type of null xs is bool which matches the requirements of being in the ‘if’ expression.

Now we study the ‘then’ and ‘else’ expressions. The first one is the integer constant 0, so its type is int. The second expression, hd xs must then unify with int. The parameter type of hd is \(t_2\,\mathtt{list}\), and xs is now thought to have type \(t_1\,\mathtt{list}\). These unify by adding the substitution \(\{t_1 = t_2\}\) (or the reverse). Applying that substitution to the facts we know so far:

alice: \(t_2\,\mathtt{list}\to t_4\)
xs: \(t_2\,\mathtt{list}\)

The return type of hd xs is \(t_2\).

Now, since one branch of the if returns int and the other branch returns \(t_2\), these types must unify. They do so by setting \(\{t_2 = \mathtt{int}\}\). Applying that substitution:

alice: \(\mathtt{int}\;\mathtt{list}\to t_4\)
xs: \(\mathtt{int}\;\mathtt{list}\)

Finally, because the if is the last expression in the definition of alice, the return type of alice (\(t_4\)) must unify with the type of the then/else branches (int). So that produces the substitution \(\{t_4 = \mathtt{int}\}\). Therefore, the final conclusion of type inference on this function is:

alice: \(\mathtt{int}\;\mathtt{list}\to \mathtt{int}\)
xs: \(\mathtt{int}\;\mathtt{list}\)

Below is a transcript of pasting the definition of alice into the SML interactive system, and then trying it out with different lists of integers.

Standard ML of New Jersey v110.79 [built: Sat Nov 21 15:48:37 2015]
- fun alice xs = if null xs then 0 else hd xs ;
val alice = fn : int list -> int
- alice [];
val it = 0 : int
- alice [3,4,5];
val it = 3 : int
- alice [8,2];
val it = 8 : int

Inference exercises:

Determine the types of these functions. A key providing the types of library functions is below the problems.

```
fun borp ts = map explode ts
```

fun crow xs =
  if null xs then 1
  else hd xs * crow (tl xs)

fun down x = if x=0 then [] else x :: down (x-1)

```
fun edgar n = crow (down n)
```

And here is the key of library functions used above.

map: ('t6 -> 't7) -> 't6 list -> 't7 list: applies a function to each element of a list, returning the results as a list.
explode: string -> char list: separates a string into a list of individual characters.
null: 't8 list -> bool: tests whether the list is empty
hd: 't9 list -> 't9: returns the first element of the list
tl: 't10 list -> 't10 list: returns the tail of a list, that is all except the first element.
=: The equals sign in x=0 requires that the left and right expressions have the same type, and it returns the type bool.
[] is the empty list, which has type 't11 list.
:: is an operator which constructs a new list from the left element and the tail element. Its type is 't12 * 't12 list -> 't12 list.

PDF

Type inference