We are working our way down through the innards of the compiler. Having studied parsing and type checking, we now look at intermediate representations (IR). In a typical compiler, the program being compiled will go through these different representations:

Source text
Parse tree
Abstract syntax tree
Intermediate representation
Target/object code

The transformations leading up to the IR are collectively called the front end of the compiler. The transformation from the IR to the object code (whether native or just another programming language) is called the back end. Most other optimizations take place on the IR. We can study some examples later on.

Sometimes important transformations take place in the conversion from parse tree to abstract syntax tree. These are known as syntactic sugar — syntactic elements that make programs easier to read, but don’t really add new capabilities. For example, the language Perl has a control construct called unless which is essentially the inverse of an if statement:

  unless(expression) {
      block
  }
  ## The above is equivalent to:
  if(!(expression)) {
      block
  }

This sort of transformation is easy to implement in the AST. By doing so, there is one fewer control statement to worry about translating when we reach the IR.

“Syntactic sugar causes cancer of the semi-colons.”

Alan Perlis, Epigrams on Programming, SIGPLAN Notices 17(9), 1982

One big benefit of a well-defined IR is that we can develop different front ends to support different source languages, and different back ends to generate code for different machine architectures or target languages.

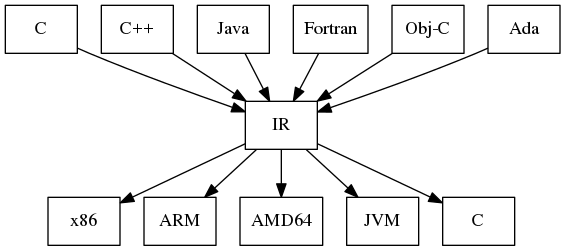
Compiler infrastructure with a common IR

The infrastructure diagram shows C as both a source language and a target language. It’s fairly common for high-level language compilers to use a subset of C as a ‘portable assembler’, and then invoke a standard C compiler to continue the work and generate native code. This minimizes the amount of work needed to produce a new compiler that can target different machine architectures.

Other popular examples of compiler systems with a common IR are:

The LLVM Compiler Infrastructure http://llvm.org/ — “a collection of modular and reusable compiler and toolchain technologies […] built around a well specified code representation known as the LLVM IR.” “It is particularly easy to invent your own language (or port an existing compiler) to use LLVM as an optimizer and code generator.”
The SUIF Compiler System http://suif.stanford.edu/ — developed at Stanford University and primarily used as a research tool to study optimization and analysis techniques.
The GNU Compiler Collection https://gcc.gnu.org/
The Microsoft Common Compiler Infrastructure http://research.microsoft.com/en-us/projects/cci/

Three-address code

The IR in a typical compiler is pretty low-level, like a portable assembly language or abstract machine code. It does not feature a wide variety of data structures, and does not support nested control structures as a source language would.

A common type of IR is known as a three-address code, so called because most instructions support three operands: one for the output and two for the inputs. In this instruction:

x := 3 * y;

The two input operands (aka addresses) are the constant 3 and the variable y. The one output address is the variable x. Here is an equivalent instruction written in the syntax of the LLVM IR:

%x = mul i32 3, %y

In that version, the multiply is designated by the opcode mul, and local variables are prefixed with %. The i32 is needed because multiplication is actually a different operation depending on the types of the operands. So i32 specifies multiplication on 32-bit integers, but LLVM also supports types like i16, f32 (32-bit float), f64, and so on.

In a three-address code, the operands can refer to named global or local variables, numeric constants, or they can be temporaries. A temporary is just a way to designate a value whose storage destination hasn’t been determined yet. It will be the job of the compiler back end to determine whether each temporary can be stored in a CPU register or somewhere in system memory, such as the stack or heap. This process is called register allocation.

In LLVM, temporaries are also designated by the percent sign, but they use numbers instead of alphabetic names:

%2 = mul i32 3, %y
%3 = mul i32 %2, 8
%4 = sub i32 %3, %2

The above sequence of instructions calculates 3*y*8-(3*y), where it stores all intermediate values into temporaries (%2, %3, %4) and does not recalculate 3*y (an optimization called common sub-expression elimination).

Flattening

In the intermediate representation, nested arithmetic expression trees must be flattened into a linear sequence of instructions. This is relatively straightforward using a bottom-up left-to-right traversal of the expression tree. Let’s consider the tree for the expression 17*2+x*(1+b)^y+x*8^2, as shown.

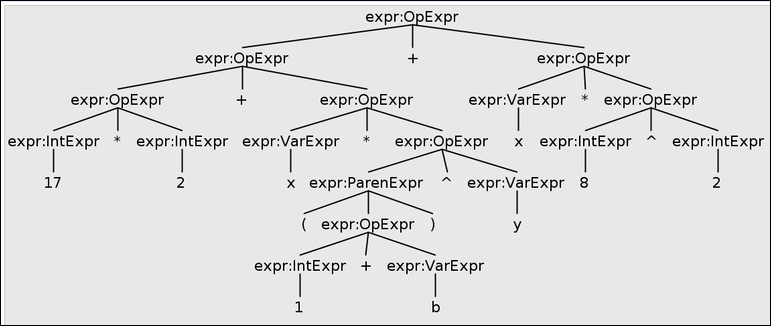
Expression tree for 17*2+x*(1+b)^y+x*8^2 in the Calc language

As we visit each OpExpr node, we allocate a new temporary variable (by just using an integer counter), then emit the operator instruction using the addresses (temporaries, variables, or constants) provided by that node’s left and right children. Here is the resulting 3-address code:

t1 := 17 *  2
t2 :=  1 +  b
t3 := t2 ^  y
t4 :=  x * t3
t5 := t1 + t4
t6 :=  8 ^  2
t7 :=  x * t6
t8 := t5 + t7

(We’ve assumed that the exponentiation operator ^ is built in to our intermediate representation. On some systems, we would need to compile it as a call to a function like pow() in C’s math.h library.)

Conditional execution

Flattening the tree becomes a little more difficult when there are conditional or iterative computations. Consider this Calc-language statement that could be part of a program to calculate the Collatz sequence:

y = if n%2=0 then x/2 else 3*x+1

(We’re using the % sign for the modulus operator.)

    t1 :=  n %  2    # if-expression
    t2 := t1 eq 0
    ifZ t2 L1        # if t2 is zero, jump to label L1
    t3 :=  x /  2    # then-expression
    t6 := t3
    jump L2
L1: t4 :=  3 *  x    # else-expression
    t5 := t4 +  1
    t6 := t5
L2: y  := t6         # assignment (after then or else)

Basic block

Within an IR, a sequence of ‘straight-line’ instructions is called a basic block. Formally, a basic block has just one entry (the first instruction in the block) and one exit (the last instruction).

TODO: examples and exercises for splitting code into basic blocks.

PDF

Intermediate representations

Three-address code

Flattening

Conditional execution

Basic block