CS664 - Assignment 5

For assignment 5, we will extend the calculator language and its type checker (described in the type checking notes) in the following ways.

We add Boolean values true and false to the language:

expr : …
     | bool                                         #BoolExpr
     ;

bool : 'true'
     | 'false'
     ;

We add a Boolean NOT operator (!) at the same precedence as numeric negation:
```
expr : op=('-'|'!') expr                            #NegExpr
     | ...
```

We add relational operators that compare numbers and produce a Boolean value:

expr : …
     | left=expr op=('<'|'<='|'>'|'>=') right=expr  #OpExpr
     | …

We add equality (=) and not-equals (<>) operators that can compare numbers or Booleans, and produce a Boolean:
```
expr : …
     | left=expr op=('='|'<>') right=expr           #OpExpr
     | …
```
We add a conditional expression that takes three sub-expressions. If the first one evaluates to true, it evaluates the second expression; otherwise it evaluates the third.
```
expr : …
     | 'if' expr 'then' expr 'else' expr            #IfExpr
     | …
```
We now will support implicit coercion from values of type INT to type FLOAT, which means we no longer need the float() function to do that explicitly. We refer to INT and FLOAT as numeric types. The BOOL type should not automatically convert to INT or FLOAT. It is not a numeric type.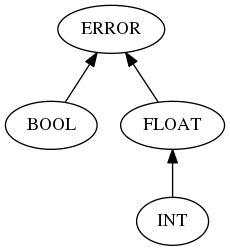

Type hierarchy, useful for calculating the least upper bound of two types.
We support the following functions:
- floor : (FLOAT) → INT
- sqrt : (FLOAT) → FLOAT
- log : (FLOAT, FLOAT) → FLOAT
where the log function takes the input number followed by the base of the logarithm. So we would code log(35,2) for \(\log_2(35) \approx 5.12928301694\) or log(256,10) for \(\log_{10}(256) \approx 2.40823996531\).

The above grammatical changes have already been made in src/main/antlr/CalcLang.g4 in the assn5 project of the public repository. Your task is to update the type checker to implement the typing rules appropriately. Specifically:

Add a BOOL entry to the Type enumeration.
Obviously, the values true and false should have type BOOL.

\[\frac{}{\Gamma\vdash\texttt{true}:\texttt{BOOL}}\qquad \frac{}{\Gamma\vdash\texttt{false}:\texttt{BOOL}}\]
The numeric negation operator (unary -) should be applied only to numeric types, not to Booleans. Conversely, the Boolean NOT operator (unary !) should be applied only to Booleans, not to numeric types. In each case, it does not change the type of the operand.

\[\frac{\Gamma\vdash \texttt{e} : \texttt{INT}} {\Gamma\vdash \texttt{-e} : \texttt{INT}} \qquad \frac{\Gamma\vdash \texttt{e} : \texttt{FLOAT}} {\Gamma\vdash \texttt{-e} : \texttt{FLOAT}} \qquad \frac{\Gamma\vdash \texttt{e} : \texttt{BOOL}} {\Gamma\vdash \texttt{!e} : \texttt{BOOL}}\]

Note: the horizontal bar in this notation represents logical implication (also known as ‘if-then’). The left-most rule is read “if the environment \(\Gamma\) (gamma) entails that expression e has type INT, then the same environment entails that the expression -e has type INT.”
The five arithmetic operators (^, *, /, +, -) work on any numeric operands, but not Booleans. The result type is the least upper bound (LUB) of the two operand types. So an INT plus an INT produces an INT, but a FLOAT plus an INT produces a FLOAT. The typing rule shows the + operator, but the same rule applies to all five of them.

\[\frac{\Gamma\vdash e_1 : \tau_1 \qquad \Gamma\vdash e_2 : \tau_2 \qquad \tau_1\in\{\texttt{INT},\texttt{FLOAT}\} \qquad \tau_2\in\{\texttt{INT},\texttt{FLOAT}\} } {\Gamma\vdash e_1\texttt{+}e_2 : \mathit{LUB}(\tau_1,\tau_2)} \]

Note: in this rule, we’re using the Greek letter \(\tau\) “tau” to represent one of our types, and we use subscripts on \(\tau\) and on \(e\) to distinguish between possibly-different types and expressions. The least upper bound \(\mathit{LUB}(\tau_1,\tau_2)\) is determined from the type hierarchy in the figure above.
The four relational operators (<, <=, >, >=) work on any numeric operands, but not Booleans; however the result type is always Boolean. The typing rule shows the < operator, but the same rule applies to all four of them.

\[\frac{\Gamma\vdash e_1 : \tau_1 \qquad \Gamma\vdash e_2 : \tau_2 \qquad \tau_1\in\{\texttt{INT},\texttt{FLOAT}\} \qquad \tau_2\in\{\texttt{INT},\texttt{FLOAT}\} } {\Gamma\vdash e_1\texttt{<}e_2 : \texttt{BOOL}} \]

Note: another way to specify \(\tau\in\{\texttt{INT},\texttt{FLOAT}\}\) is to write \(\mathit{LUB}(\tau,\texttt{FLOAT}) = \texttt{FLOAT}\).
The two equality operators (=, <>) work on any compatible types, whether numeric or Boolean. The result type is always Boolean. The typing rule shows the = operator, but the same rule applies to both.

\[\frac{\Gamma\vdash e_1:\tau_1 \qquad \Gamma\vdash e_2:\tau_2 \qquad \mathit{LUB}(\tau_1,\tau_2)\not=\texttt{ERROR}} {\Gamma\vdash e_1\texttt{=}e_2 : \texttt{BOOL}}\]
The first sub-expression in a conditional expression must have type BOOL, and the types of the two branches must have a least upper bound that is not ERROR.

\[\frac{\Gamma\vdash e_1:\texttt{BOOL}\qquad \Gamma\vdash e_2:\tau_2\qquad \Gamma\vdash e_3:\tau_3\qquad \mathit{LUB}(\tau_2,\tau_3)\not=\texttt{ERROR}} {\Gamma\vdash \texttt{if }e_1\texttt{ then }e_2\texttt{ else }e_3 : \mathit{LUB}(\tau_2,\tau_3)} \]
Here are the typing rules for the functions, using the least upper bound calculation to allow implicit coercions.

\[\frac{\Gamma\vdash e:\tau \qquad \mathit{LUB}(\tau,\texttt{FLOAT})=\texttt{FLOAT}} {\Gamma\vdash\texttt{floor(}e\texttt{)} : \texttt{INT}}\]

\[\frac{\Gamma\vdash e:\tau \qquad \mathit{LUB}(\tau,\texttt{FLOAT})=\texttt{FLOAT}} {\Gamma\vdash\texttt{sqrt(}e\texttt{)} : \texttt{FLOAT}}\]

\[\frac{\Gamma\vdash e_1:\tau_1 \qquad \Gamma\vdash e_2:\tau_2 \qquad \mathit{LUB}(\tau_1,\mathit{LUB}(\tau_2,\texttt{FLOAT}))=\texttt{FLOAT}} {\Gamma\vdash\texttt{log(}e_1,e_2\texttt{)} : \texttt{FLOAT}}\]
The text files within the tests/ sub-directory represent test cases. You can run them using the main program class TestTypeChecker. All of the files should parse correctly. The files in tests/bad contain type errors that your type checker should report. The files in tests/good contain no type errors, so your type checker should accept them. (The TypeCheckingVisitor increments its errors field each time the error() method is called to report an error. So for all the files in tests/good we expect errors == 0; and for all the files in tests/bad we expect errors > 0.)

PDF