Most programming languages support some notion of types and type-checking. If parsing is syntactic analysis, then type checking is semantic analysis. (Syntax refers to the form of a phrase, whereas semantics refers to its meaning.)

What is a type?

In mathematical logic, types were introduced to prevent Russell’s paradox by restricting set-building operations. Similarly, in programming languages, types prevent the programmer from accidentally (or intentionally) writing code that would be unsafe or nonsense.

Essentially, a type defines a set of values. For example, the type integer might correspond to \(\mathbb{Z}\), the set of all integers, or the type word16 might correspond to the set of non-negative 16-bit integers: \(\{x \;|\; x\in\mathbb{Z} \wedge 0 \le x < 65536 \}\).

Types can be primitive such as int, float, and bool or they can be composite – that is, they are composed by applying type operators to other types. A common example of a type operator in many programming languages is the array type, often designated with square brackets []. This is not a type on its own, but rather can be applied as a postfix operator to other types, such as int[] for an array of integers or bool[] for an array of booleans. And since those are types, we can apply the array operator to either of them again, producing int[][] for an array of arrays of integers.

Types can also be built-in or user-defined. For example in C++ or Java, a class declaration introduces (among other things) a new type.

class User {
  public:
    string firstName;
    string lastName;
    int birthYear;
};

We can now refer to User to declare composite variables such as:

User[] roster;          // A list of Users
User[][] seatingChart;  // A 2-dimensional grid of Users

Type checking can be static or dynamic. A static type checker performs semantic analysis at compile time, so it can alert us about improper uses of values before running the program.

For example, in Java it doesn’t make any sense to divide a string by an integer:

System.out.println("Forty-two" / 7);

So the Java compiler says:

Error:(5, 31) java: bad operand types for binary operator '/'
  first type:  java.lang.String
  second type: int

In contrast, dynamic type checking happens at run time. Dynamic checking is used in languages such as Python and Ruby. If we convert the division example to Python and run it,

print("Forty-two" / 7)

the Python interpreter will report:

TypeError: unsupported operand type(s) for /: 'str' and 'int'

This looks like pretty much the same error as in Java. The difference is that the error only happens if and when the erroneous code is executed. If it is avoided somehow, then the error is not triggered. Consider this Python script:

from random import random
if random() < 0.5:
    print("Forty-two" / 7)
else:
    print("Whew, we dodged a bullet!")

The imported random() function produces a random floating-point value between 0 and 1, so random() < 0.5 approximates flipping a coin. About half the time this script will run to completion with no errors, and the other half of the runs will trigger the type error:

% python dynamic_error.py
Whew, we dodged a bullet!

% python dynamic_error.py
Whew, we dodged a bullet!

% python dynamic_error.py
TypeError: unsupported operand type(s) for /: 'str' and 'int'

% python dynamic_error.py
TypeError: unsupported operand type(s) for /: 'str' and 'int'

% python dynamic_error.py
Whew, we dodged a bullet!

Because this is a compilers course, we’ll concern ourselves only with static type checking.

Type-checking visitor

Let’s explore a simple technique for type checking by using a visitor to walk the parse tree. We’ll use the calculator language, but this time let’s define distinct lexical rules for integers and floats:

INT  : [0-9]+;
FLOAT: [0-9]+ '.' [0-9]* ('e' '-'? [0-9]+)?;

So integers are non-empty sequences of digits. The floats in this language require a non-empty sequence of digits followed by a dot. Then there are optionally additional digits and an exponent. So these are all valid float values:

3.
0.5
3.14159
29.e-8
0.001e72

but these are not:

3
.5
.001e72

Then we have distinct IntExpr and FloatExpr rules in the expression grammar:

expr : '-' expr                                     #NegExpr
     | <assoc=right> left=expr op='^' right=expr    #OpExpr
     | left=expr op=('*'|'/') right=expr            #OpExpr
     | left=expr op=('+'|'-') right=expr            #OpExpr
     | ID '(' expr (',' expr)* ')'                  #FunExpr
     | '(' expr ')'                                 #ParenExpr
     | INT                                          #IntExpr
     | FLOAT                                        #FloatExpr
     | ID                                           #VarExpr
     ;

Notice that compared to previous versions of this language, we also added an OpExpr for the exponentiation operator, ‘^’. It is right-associative so that 2^2^2^3 is grouped as 2^(2^(2^3)), representing the mathematical notation \(2^{2^{2^3}}\).

We also added a FunExpr for function calls. This supports syntax with one or more comma-separated arguments. So examples of function calls would be:

sin(theta)
floor(15.2)
sum(3, 5, 8, 13)

This language will have only primitive types for integers and floats – no composite types. Let’s represent our types as an enumeration:

public enum Type {
    INT,
    FLOAT,
    ERROR
}

We’ll explain the reason for the ERROR type in a subsequent section.

Now we’ll define a visitor to do our type checking – this is all implemented in the typecheck project in the public repository.

public class TypeCheckingVisitor extends CalcLangBaseVisitor<Type> {

The super-class is instantiated with <Type> to specify that all the visit methods should return the Type of the expression tree that they traverse. For statements (like print) that don’t return any value, we can use null. (Alternatively, we could define VOID in our enum and use that.)

Two of the simplest kinds of expressions to handle are the IntExpr and FloatExpr – those types are obvious.

    @Override
    public Type visitIntExpr(CalcLangParser.IntExprContext ctx) {
        return Type.INT;  // An integer expression has type INT
    }

    @Override
    public Type visitFloatExpr(CalcLangParser.FloatExprContext ctx) {
        return Type.FLOAT;  // A float expression has type FLOAT
    }

Another expression case that’s pretty easy is negation. The negation operator can be applied either to an int (-5) or to a float (- 3.14) and it doesn’t change the type.

    @Override
    public Type visitNegExpr(CalcLangParser.NegExprContext ctx) {
        return ctx.expr().accept(this);
    }

In that method, ctx.expr() is used to refer to the sub-expression of the NegExpr, and then accept(this) means “continue to traverse that subtree using this same visitor.” So whatever type the sub-expression has, the negation expression will also have. (If our language had non-numeric types, we’d have to be more restrictive here — negation can be applied to any signed numeric type but not, for example, to strings.)

Before moving on, we’ll implement a way to help us visualize what’s going on with our type checker. The trace method defined below prints out a fragment of the parse tree along with its type.

    private Type trace(ParseTree ctx, Type type) {
        System.err.printf("∅ ⊢ %s : %s\n", ctx.getText(), type);
        return type;
    }

We ask it to return the type so we can employ it very conveniently as part of the return statement in the visit methods:

    // These three methods *replace* the above implementations.

    @Override
    public Type visitIntExpr(CalcLangParser.IntExprContext ctx) {
        return trace(ctx, Type.INT);
    }

    @Override
    public Type visitFloatExpr(CalcLangParser.FloatExprContext ctx) {
        return trace(ctx, Type.FLOAT);
    }

    @Override
    public Type visitNegExpr(CalcLangParser.NegExprContext ctx) {
        return trace(ctx, ctx.expr().accept(this));
    }

Now as our visitor traverses a program like print -4+5*6.9; it will output (not including the line comments that start with #):

∅ ⊢ 4 : INT         # in visitIntExpr
∅ ⊢ -4 : INT        # in visitNegExpr
∅ ⊢ 5 : INT         # in visitIntExpr
∅ ⊢ 6.9 : FLOAT     # in visitFloatExpr

The notation we’re using here is from type theory, a branch of mathematical logic. The statement \(\emptyset\vdash \mathtt{4} : \mathtt{INT}\) should be read “in the empty environment, we can prove that 4 has type INT.” The symbol \(\vdash\) is called the turnstile and it generally means proves or entails. We’ll see later what else can be used in place of the empty environment, \(\emptyset\).

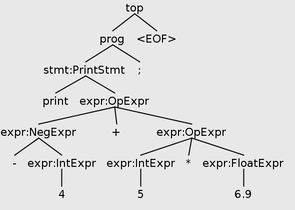
For reference, this is the parse tree of print -4+5*6.9;

We’ve handled parse tree nodes near the leaves: IntExpr, FloatExpr, and NegExpr. But what about OpExpr which applies one of the five operators (^, *, /, +, or -)?

In this version of the calculator language, we’ll be very strict about type-checking the operators. They can all be applied to INT or FLOAT, but we won’t be able to mix and match – we’re either doing integer arithmetic or floating-point arithmetic. For example,

5 + 3 is type-correct because both expressions are integers, so it produces the integer 8
5.0 + 3. is type-correct because both expressions are floats, so it produces the float 8.
5 + 3. is a type error, because we cannot directly add an integer and a float
19 / 2 is type-correct because both expressions are integers, so it produces the integer 9 — this is known in C++ and Java as integer division
19 / 2.0 is a type error, because we cannot directly divide an integer by a float

Later on we will explore how to allow implicit coercions from INT to FLOAT as supported by C++ and Java.

Until then, we can use the new function-call syntax to provide two expressions for explicitly converting between integers and floats:

floor(19.8) – this function expects a float and returns the largest integer less than that float, so the result here would be the integer 19
float(4) – this function expects an integer and returns the corresponding float, so the result here would be 4.

As a further example, we can do the floating-point division \(\frac{19}{2}\) by writing float(19)/2.0 or float(19)/float(2) or 19./float(2).

Here, then, is the basic strategy for type-checking the operators:

    @Override
    public Type visitOpExpr(CalcLangParser.OpExprContext ctx) {
        Type leftType = ctx.left.accept(this);
        Type rightType = ctx.right.accept(this);
        if(leftType == rightType) {
            return trace(ctx, leftType);
        }
        else {
            return typeMismatch(ctx, leftType, rightType);
        }
    }

We use the ctx.left.accept(this) to recursively type-check the left (and then right) sub-expression. Then if those two are the same type (leftType == rightType), we return it. Otherwise, we report the type mismatch using a helper method:

    private Type typeMismatch(ParseTree ctx, Type t1, Type t2) {
        System.err.printf("Error: type mismatch: %s vs %s in %s\n",
                    t1, t2, ctx.getText());
        return trace(ctx, Type.ERROR);
    }

So in the program print 19/2.0; the type checker would say:

∅ ⊢ 19 : INT
∅ ⊢ 2.0 : FLOAT
Error: type mismatch: INT vs FLOAT in 19/2.0
∅ ⊢ 19/2.0 : ERROR

Or in a type-correct program like print 19/2, it would report the type of the operator expression after the types of its sub-expressions.

∅ ⊢ 19 : INT       # in visitIntExpr
∅ ⊢ 2 : INT        # in visitIntExpr
∅ ⊢ 19/2 : INT     # in visitOpExpr

Make sure to define visitParenExpr also, to allow types to be propagated through parenthesized expressions, such as print (1+2)*3;:

∅ ⊢ 1 : INT        # in visitIntExpr
∅ ⊢ 2 : INT        # in visitIntExpr
∅ ⊢ 1+2 : INT      # in visitOpExpr
∅ ⊢ (1+2) : INT    # in visitParenExpr
∅ ⊢ 3 : INT        # in visitIntExpr
∅ ⊢ (1+2)*3 : INT  # in visitOpExpr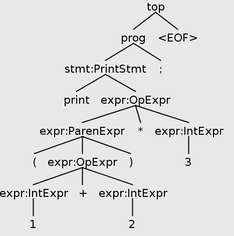

For reference, the parse tree for print (1+2)*3;. You can see that the post-order traversal would be Int(1), Int(2), Op(+), Paren, Int(3), Op(*), as traced by the type checking visitor.

Reporting error location

Error messages are always more useful if we can pinpoint the region of code in which they occur. The CommonTokenStream class provided by ANTLR caches the sequence of tokens generated by the lexer, and each token also records its location (line number and column position) in the code.

When we identify a type error in a sub-tree, we can use getSourceInterval() to identify the starting and ending tokens. It is used as follows, where ctx is a ParseTree or any of its node subclasses, such as OpExprContext or ParenExprContext; and tokens is a CommonTokenStream.

        Interval interval = ctx.getSourceInterval();
        Token first = tokens.get(interval.a);
        Token last = tokens.get(interval.b);

And then on the Token objects we can call getLine() and getCharPositionInLine(). Here’s a complete error-reporting helper method that uses these facilities to pinpoint the character or range of characters where the error occurred.

    private void error(ParseTree ctx, String message) {
        errors++;
        Interval interval = ctx.getSourceInterval();
        Token first = tokens.get(interval.a);
        Token last = tokens.get(interval.b);
        if(first == last) {
            System.err.printf("%d.%d",
                    first.getLine(),
                    first.getCharPositionInLine()
            );
        } else {
            System.err.printf("%d.%d-%d.%d",
                    first.getLine(),
                    first.getCharPositionInLine(),
                    last.getLine(),
                    last.getCharPositionInLine()
            );
        }
        System.err.printf(": Error: %s\n", message);
    }

The error() method uses if(first == last) to distinguish whether the error is related to just one token (such as an undefined variable) or a range of tokens (such as a type mismatch in a binary operator).

In the sample code for TypeCheckingVisitor, the error() method is called by typeMismatch to report conflicting types, by checkNumArgs if a function is called with the wrong number of arguments, by visitVarExpr if the variable is undefined, and by visitFunExpr if a function name is unknown.

Cascading type errors

When a type error occurs deep inside a sub-expression, there is a danger of having that error cascade to produce a series of other error messages. Often (but not always) these superfluous errors are not helpful, because fixing the first one will automatically resolve them.

Here’s an example using a series of addition operators, which are left-associative. The bottom-most (left-most) addition is 1.0+2, which should produce a type error because the left side is a FLOAT and the right side is an INT. So after reporting that error, what should we return for the type of 1.0+2? Our choice will affect subsequent analysis the rest of the way up the tree!

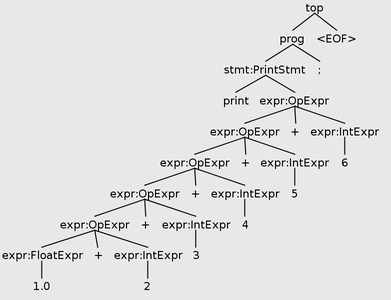
Parse tree for print 1.0+2+3+4+5+6;

If we choose to say that 1.0+2 is a FLOAT, then the error cascades. In the parent operator, it will report a second type mismatch because the left side of that addition is a FLOAT and the right side is an INT. And so on, up the tree.

If we choose to say that 1.0+2 is an INT, then we get lucky and there is no cascade, because that matches the expected INT type of the rest of the sum.

But how to choose? Always returning either the left type (FLOAT in this example) or the right type (INT) will behave badly in some cases and okay in others. All we need to do is swap the expressions in the bottom-most addition and we get the opposite behavior.

An alternative is to use a specially-designated ERROR type. Marking an expression as having type ERROR indicates “there was a type error here, so we don’t know what type it should be.” That alone will not prevent the cascade. Instead, it will just continue to report that ERROR does not match other types the rest of the way up the tree.

∅ ⊢ 1.0 : FLOAT
∅ ⊢ 2 : INT
1.6-1.10: Error: type mismatch: FLOAT vs INT in 1.0+2
∅ ⊢ 1.0+2 : ERROR
∅ ⊢ 3 : INT
1.6-1.12: Error: type mismatch: ERROR vs INT in 1.0+2+3
∅ ⊢ 1.0+2+3 : ERROR
∅ ⊢ 4 : INT
1.6-1.14: Error: type mismatch: ERROR vs INT in 1.0+2+3+4
∅ ⊢ 1.0+2+3+4 : ERROR
∅ ⊢ 5 : INT
1.6-1.16: Error: type mismatch: ERROR vs INT in 1.0+2+3+4+5
∅ ⊢ 1.0+2+3+4+5 : ERROR
∅ ⊢ 6 : INT
1.6-1.18: Error: type mismatch: ERROR vs INT in 1.0+2+3+4+5+6
∅ ⊢ 1.0+2+3+4+5+6 : ERROR

However, if we implement our reporting of type mismatches more carefully, we can simply suppress any type mismatch errors where one of the types in conflict is ERROR. Then only the bottom-most error is reported, and the rest are ignored.

Below is the definition of a typeMismatch helper that prints an error only if we haven’t already reported an error in a sub-expression.

    private Type typeMismatch(ParseTree ctx, Type t1, Type t2) {
        if(t1 != Type.ERROR && t2 != Type.ERROR) {   // prevent cascade
            error(ctx, String.format("type mismatch: %s vs %s in %s",
                    t1, t2, ctx.getText()));
        }
        return trace(ctx, Type.ERROR);
    }

Now only the FLOAT vs INT conflict is reported, and the remaining ERROR vs INT conflicts are suppressed. The typing judgments are just for visualizing and debugging; in a real production compiler they’d be turned off so they don’t count as error messages.

∅ ⊢ 1.0 : FLOAT
∅ ⊢ 2 : INT
1.6-1.10: Error: type mismatch: FLOAT vs INT in 1.0+2
∅ ⊢ 1.0+2 : ERROR
∅ ⊢ 3 : INT
∅ ⊢ 1.0+2+3 : ERROR
∅ ⊢ 4 : INT
∅ ⊢ 1.0+2+3+4 : ERROR
∅ ⊢ 5 : INT
∅ ⊢ 1.0+2+3+4+5 : ERROR
∅ ⊢ 6 : INT
∅ ⊢ 1.0+2+3+4+5+6 : ERROR

Even with this cascade suppression, it’s still possible for one expression to produce more than one error, as long as the nodes containing the mismatch are “cousins,” rather than in an ancestor/descendant relationship. For example, consider the tree for 6.2^3*8+7*4^2.0. Each of the exponent OpExpr(^) nodes contains a type error, but they are not in an ancestor relationship so both will be reported.

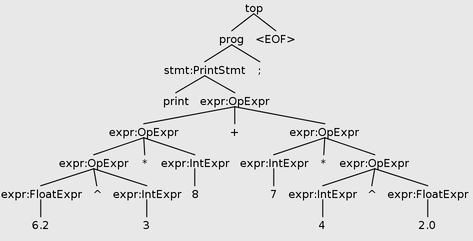
Parse tree for print 6.2^3*8+7*4^2.0; which contains type errors down both branches.

∅ ⊢ 6.2 : FLOAT
∅ ⊢ 3 : INT
1.6-1.10: Error: type mismatch: FLOAT vs INT in 6.2^3
∅ ⊢ 6.2^3 : ERROR
∅ ⊢ 8 : INT
∅ ⊢ 6.2^3*8 : ERROR
∅ ⊢ 7 : INT
∅ ⊢ 4 : INT
∅ ⊢ 2.0 : FLOAT
1.16-1.18: Error: type mismatch: INT vs FLOAT in 4^2.0
∅ ⊢ 4^2.0 : ERROR
∅ ⊢ 7*4^2.0 : ERROR
∅ ⊢ 6.2^3*8+7*4^2.0 : ERROR

Symbol table

Our type checker for the calculator language is not complete until it supports variables. Calculator programs are a sequence of statements, and a statement is either a print or a variable assignment:

pi = 3.14159;
r = 7.1;
area = pi * r^2;
print area;

The lifetime and scope of each variable is the rest of the program that follows its first assignment. Thanks to that simple rule and the absence of loops, it’s easy to deduce the type of each variable from the expression on the right side of the assignment. In this program:

k = 3;
j = 4.1;
print j+k;

we deduce that k is an INT and j is a FLOAT. Then, on line 3 we observe that j+k is a type mismatch.

Previously, our typing judgments looked like ∅ ⊢ E : T, which we read as “in the empty environment, we can prove that expression E has type T.” To keep track of the types of variables, we extend the empty environment to a mapping from variable names to their types. So {x=INT} ⊢ x : INT means “in an environment where variable x has type INT, the expression x has type INT.” This seems indeed like an obvious conclusion, but these environments will help us track variable types as we traverse the program tree. For the program above, the type checker outputs:

{} ⊢ 3 : INT
{k=INT} ⊢ 4.1 : FLOAT
{j=FLOAT, k=INT} ⊢ j : FLOAT
{j=FLOAT, k=INT} ⊢ k : INT
3.6-3.8: Error: type mismatch: FLOAT vs INT in j+k
{j=FLOAT, k=INT} ⊢ j+k : ERROR

You can see that when we type-check the sub-expression 4.1 (line 2), the environment already contains k=INT. Then when we type-check the usage of j on line 3, the environment has {j=FLOAT, k=INT} so we conclude that j has type FLOAT.

The environment is also called a symbol table. For now, the symbol table can just be represented by HashMap<String,Type>, a mapping from names to types. Later when we want to support scopes and other attributes of variables, the symbol table representation will need to be more sophisticated.

Here are the additional fields and overrides needed in the TypeCheckingVisitor:

    private HashMap<String, Type> symbols = new HashMap<>();

    @Override
    public Type visitAssignStmt(CalcLangParser.AssignStmtContext ctx) {
        String var = ctx.ID().getText();
        Type type = ctx.expr().accept(this);
        symbols.put(var, type); // Add to symbol table
        return null;
    }

    @Override
    public Type visitVarExpr(CalcLangParser.VarExprContext ctx) {
        String var = ctx.ID().getText();
        Type type = symbols.get(var);  // Look up in symbol table
        if(type == null) {
            error(ctx, "undefined variable: " + var);
            return trace(ctx, Type.ERROR);
        }
        else {
            return trace(ctx, type);
        }
    }

Coercions and subtypes

Most languages support converting values from one type to another, either implicitly or explicitly. An explicit coercion is one that is specifically coded in the program text. For example, the float(x) function is an explicit coercion from an integer value to a floating-point value, and floor(x) is an explicit coercion from floating-point to integer.

An implicit coercion is one that happens automatically, without having to be coded into the program text. The type checker for the calculator language described above does not support implicit coercions, but many languages do. Typically, an implicit coercion is supported when there would be no loss of data. For example, in C/C++/Java we have an implicit coercion from float to double because that just increases the precision without loss. But a conversion from double to float would be problematic because we would lose precision. Similarly, converting from float to int would lose data because a value like 3.14 would be truncated to just 3; but coercion from int to float could be supported implicitly.

A good formal way to represent possible coercions is as a partially-ordered set, or lattice. We can draw the lattice with arrows to represent that one type is a subtype of another. Generally, implicit coercions are allowed in the direction of the arrow. Subtype relationships are usually notated with the less-than-equal operator (\(\texttt{int}\le\texttt{long}\)) or variations like (\(\texttt{int}<:\texttt{long}\)) or (\(\texttt{int}\preceq\texttt{long}\)).

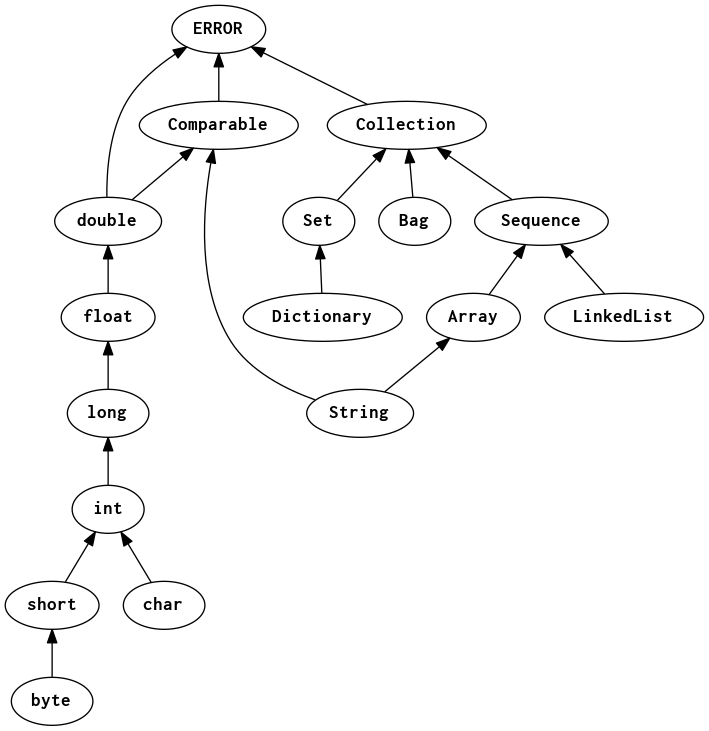
Lattice for numeric and collection types in a hypothetical programming language.

Once we have defined the lattice, we can calculate the least upper bound between any two types. The \(\mathit{LUB}(t_1,t_2)\) is the nearest type for which \(t_1\) and \(t_2\) are subtypes in the lattice. Also, every type is considered to be a subtype of itself. Here are some examples using the lattice in the figure:

\(\mathit{LUB}(\texttt{float}, \texttt{float}) = \texttt{float}\)
\(\mathit{LUB}(\texttt{double}, \texttt{int}) = \texttt{double}\)
\(\mathit{LUB}(\texttt{short}, \texttt{char}) = \texttt{int}\)
\(\mathit{LUB}(\texttt{short}, \texttt{char}) = \texttt{int}\)
\(\mathit{LUB}(\texttt{long}, \texttt{String}) = \texttt{Comparable}\)
\(\mathit{LUB}(\texttt{String}, \texttt{LinkedList}) = \texttt{Sequence}\)
\(\mathit{LUB}(\texttt{Set}, \texttt{String}) = \texttt{Collection}\)
\(\mathit{LUB}(\texttt{Array}, \texttt{byte}) = \texttt{ERROR}\)

(The least upper bound is not always defined, and can be ambiguous if there is more than one. To ensure that it is at least defined, we can add an ERROR type at the root of the lattice if there isn’t already a root. If there is more than one least upper bound, we can simply interpret that ambiguity as a type error.)

PDF