Today we’ll study parsing and understand better how the lexer and parser interact. Throughout we’ll use a tiny language for calculations similar to the Unix bc program – an arbitrary-precision calculator. Here is a first cut at the grammar:

prog → prog stm ;
prog → ε
stm → ID = expr
stm → print expr
expr → expr + expr
expr → expr - expr
expr → expr * expr
expr → expr / expr
expr → ( expr )
expr → NUM
expr → ID

So a program is a sequence of statements, each statement terminated by a semi-colon. The tree below illustrates how the two ‘prog’ rules can be applied to generate (or parse) that sequence.

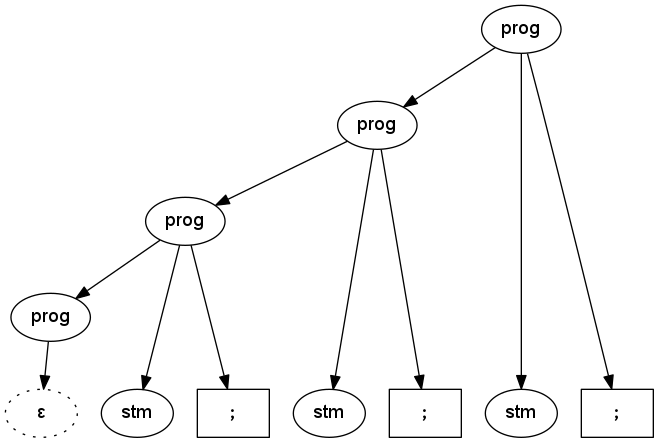
Parse tree for three semicolon-terminated statements using left-recursive grammar

Ambiguity

The expression rules are ambiguous. A grammar is unambiguous if every string in the language has a unique parse tree. But if we can generate more than one parse tree for the same string, the grammar is ambiguous. Below are some trees for expressions that illustrate ambiguity.

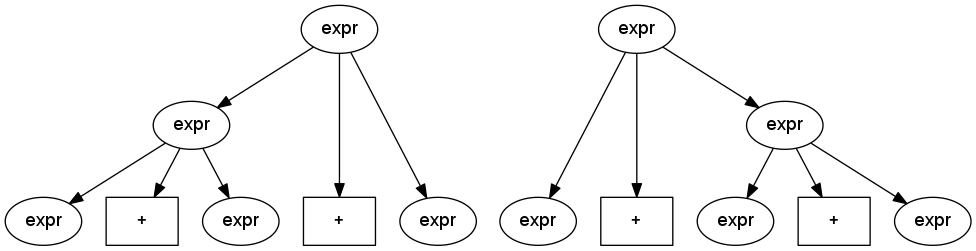
Two different parse trees (left-associative and right-associative) for the same sequence of operations

Top-down vs bottom-up

The two basic parsing strategy are top-down and bottom-up:

Top-down means we start from some root non-terminal and use the sequence of tokens to identify which grammar rules to apply. Top-down parsers are written using a technique called recursive descent, and are not that difficult to write by hand.
Bottom-up means we start from the sequence of tokens, and with each token decide whether to shift the token into a waiting buffer, or reduce the current buffer by applying a rule from the grammar. In this way, the tree is built bottom-up. So-called shift-reduce parsers are extremely tedious to write by hand. In practice, they will be generated by a tool like “yacc” or its variants.

Left recursion

One of the properties of a grammar that causes problems for recursive descent parsing is left recursion.

Each non-terminal (on the left side of an arrow ‘→’) in the grammar is implemented as a (possibly recursive) method. That method tries to distinguish between which rules to apply, based on the sequence of tokens. Then it calls other methods to handle each terminal and non-terminal on the right side of the ‘→’.

In our sample grammar, both the ‘prog’ and ‘expr’ rules are quite obviously left-recursive:

prog → prog stm ;
expr → expr + expr

That means a recursive descent approach would immediately create an infinite loop, as illustrated in the Java methods we’d derive from the above rules.

void parseProg() {
    parseProg();  // Uh-oh, unbounded recursion!
    parseStm();
    match(SEMI);
}

void parseExpr() {
    parseExpr();  // Uh-oh, unbounded recursion!
    match(PLUS);
    parseExpr();
}

There are other ways left-recursion can happen that are not as obvious as these. For one, you could have two rules that are mutually recursive:

blip → glop ;
glop → blip .

Another more subtle source of left-recursion can happen when rules are nullable, that is, they can reduce to the empty string, ‘ε’:

luke → han luke
han → void
han → ε

Because the non-terminal ’han’ is nullable, ’luke’ ends up being able to recursively call ‘luke’ without consuming any tokens – that’s the formal definition of left recursion.

Removing ambiguities and left recursion

There are a couple of techniques and heuristics that can be applied to the grammars of most programming languages in order to remove ambiguity and left recursion. Here is a rewrite of the original grammar for the calculator language, using those techniques.

prog → stm ; prog
prog → ε
stm → ID = add-expr
stm → print add-expr
add-expr → mult-expr + add-expr
add-expr → mult-expr - add-expr
add-expr → mult-expr
mult-expr → base-expr * mult-expr
mult-expr → base-expr / mult-expr
mult-expr → base-expr
base-expr → ( add-expr )
base-expr → NUM
base-expr → ID

This grammar flips around the prog rule, so that it’s right-recursive instead of left. This generates a different parse tree than before, but it doesn’t really matter – the sequence of statements is still the same.

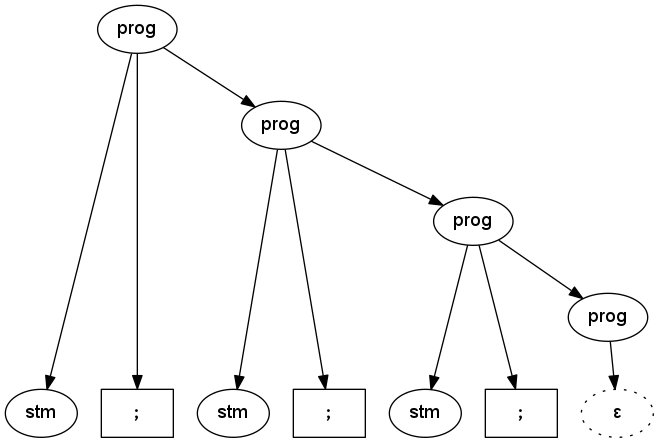
Parse tree for three semicolon-terminated statements using right-recursive grammar

Furthermore, the precedence and associativity of all the arithmetic operators are encoded into the grammar. Every string in the language has a unique parse tree specified by these rules, so it’s no longer ambiguous.

Update: unfortunately, although the above grammar is unambiguous and avoids left recursion, it also makes the operators right-associative. This can cause unexpected behavior for subtraction and division. For example, 10-2-3 produces the tree shown below, whose value will be 10-(2-3) = 10-(-1) = 11. The expected behavior is for operators to be left-associative, so then we would get (10-2)-3 = 8-3 = 5.

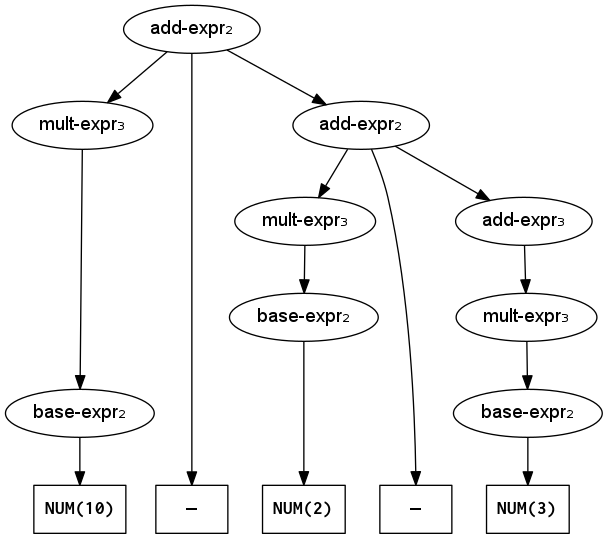
Parse tree for right-associative subtraction

The subscripts next to non-terminal names in the tree indicate which grammar rule was applied for that non-terminal. For example, add-expr₂ indicates the rule that produces the subtraction operator and add-expr₃ converts directly to a mult-expr.

There are algorithms that can take a right-associative parse tree and rewrite it to be left-associative. When we use a parser generator such as ANTLR or Bison, they can take care of associativity for you.

PDF

Parsing and grammars

Ambiguity

Top-down vs bottom-up

Left recursion

Removing ambiguities and left recursion