Register allocation
4 May 2016
IR uses potentially large number of program variables and temporaries.
Machine supports small number of registers (very fast storage).
Mapping variables/temporaries to registers is called register allocation.
If not all vars/temps can be allocated to registers, we spill one or more of them to main memory (much slower storage).
Variety of algorithms and variations:
- Chaitin (1982), based on graph-coloring (NP complete)
- George, Appel (1996), iterated register coalescing
- Poletto & Sarkar (1999), linear scan register allocation
All these rely on liveness analysis, a backwards data flow analysis.
Calculates the set of variables that are live at every point in program.
A variable is live if it holds a value that may be needed in the future.
For each statement \(s\), define \(\mathit{Gen}(s)\) as the set of variables used in \(s\) before any assignment.
Define \(\mathit{Kill}(s)\) as the set of variables assigned a value in \(s\).
Start at the exit node, where the set of live variables is empty, and work backwards.
For each statement, calculate \(\mathit{Live}_{\mathit{out}}(s)\) as the union of \(\mathit{Live}_{\mathit{in}}(t)\) for each successor \(t\).
Then calculate \(\mathit{Live}_{\mathit{in}}(s) = \mathit{Gen}(s) \cup (\mathit{Live}_{\mathit{out}}(s) - \mathit{Kill}(s))\).
When the program has loops, you may need to iterate a few times until all sets converge.
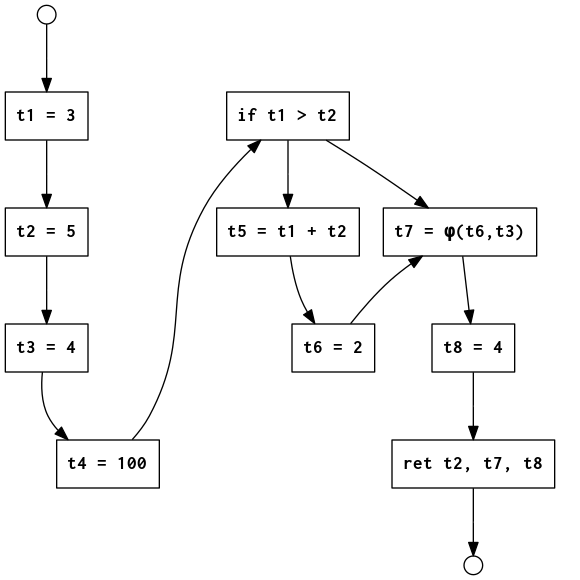
Program graph in SSA form with if-then statement
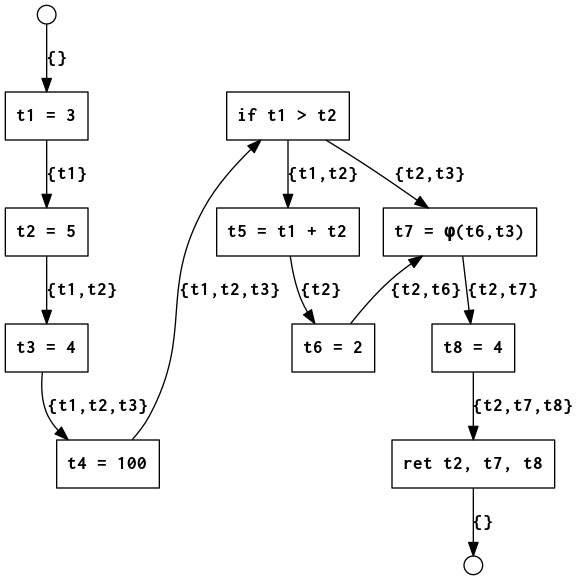
Results of liveness analysis for program in figure 1
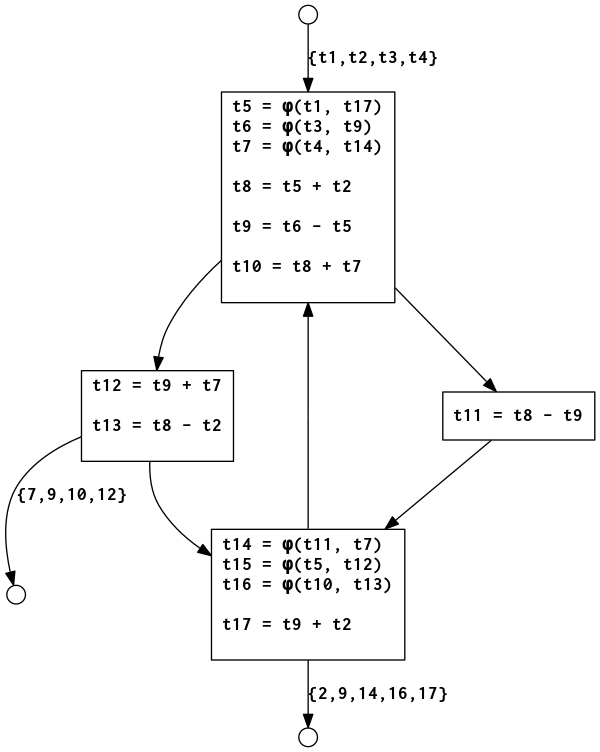
SSA program graph with loop and if-else
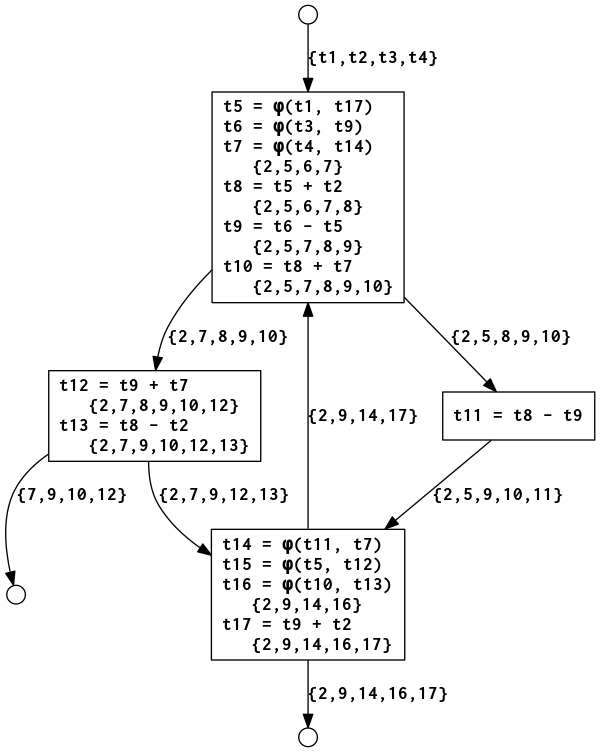
Results of liveness analysis for program in figure 3
Once we calculate \(\mathit{Live}\) sets, build an undirected graph where nodes are temporaries and edges indicate interference: two temporaries that are live at the same time.
Can also add preference edges (dotted lines) that indicate a preference for keeping two temporaries in the same register.
Preference edges are especially useful for reducing moves in \(\phi\) statements: \(t_1 = \phi(t_2,t_3)\) will generate preferences that \(t_1=t_2\) and \(t_1=t_3\).
Register allocation corresponds to a coloring of the interference graph.
Greedy algorithm for coloring: start with the highest-degree node and choose its register. Eliminate that register as a candidate from all of its neighbors. Repeat.
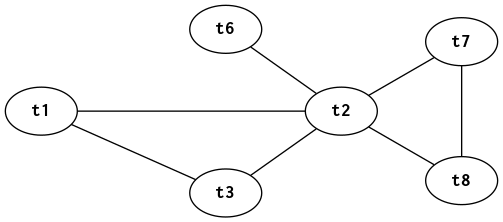
Interference graph for program in figures 1, 2
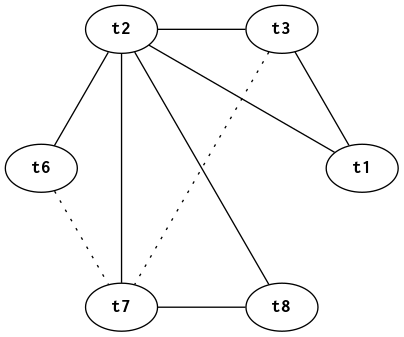
Interference graph with preference edges for program in figures 1, 2
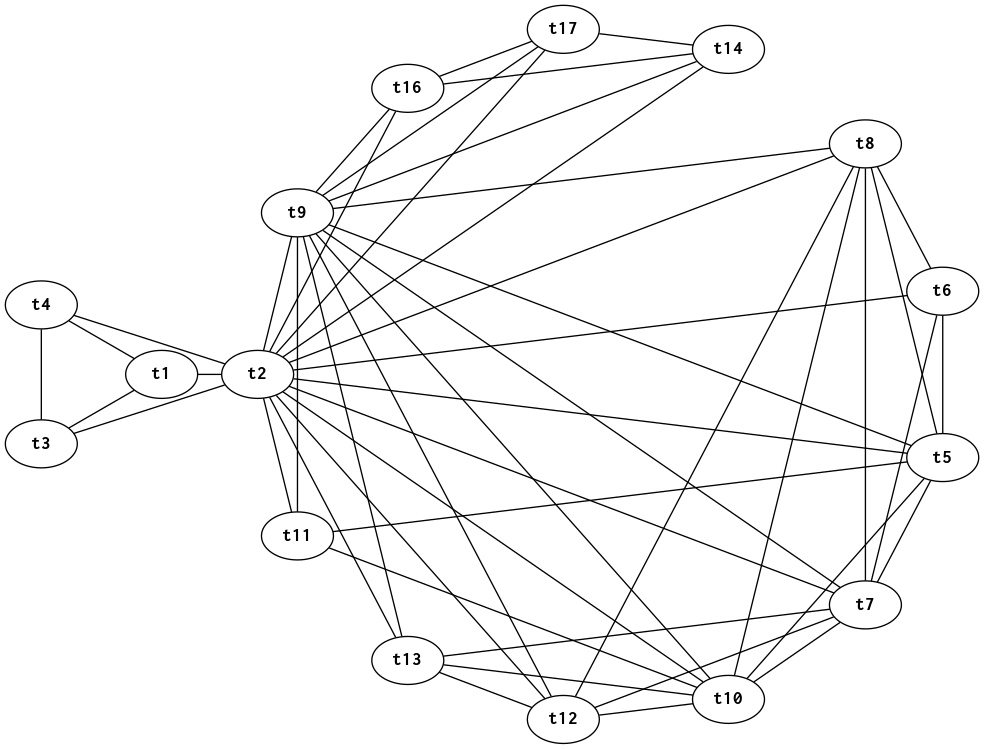
Interference graph for program figures 3, 4
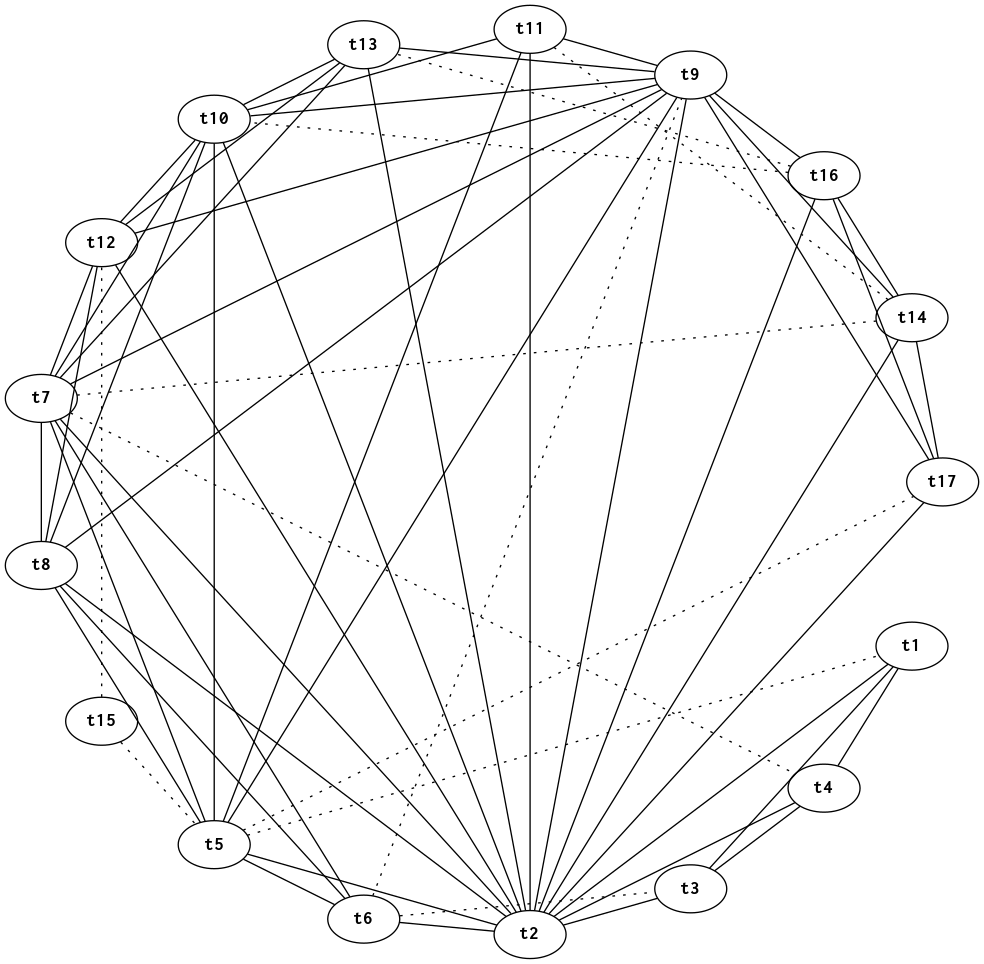
Interference graph with preference edges for program figures 3, 4