Context classes

ANTLR automatically generates heterogeneous representations of the parse trees for your grammar. The tree classes for each non-terminal are embedded within the generated parser class and inherit from other Tree classes in the ANTLR library.

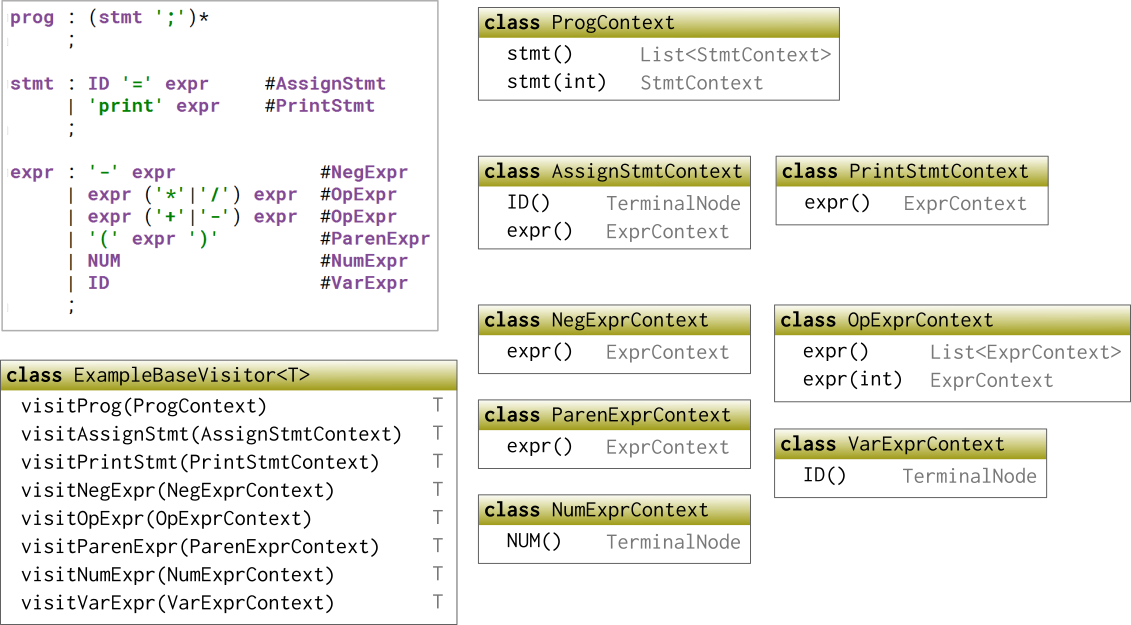
For example, let’s consider the sample grammar for the Calculator language, as shown to the left in the figure.

Example calculator grammar, and some of the classes ANTLR generates

The fragment of the grammar shown defines three non-terminals: prog representing programs, stmt representing statements, and expr representing expressions. Each one of these produces a so-called “Context” class to represent its nodes in the parse tree generated by those grammar rules. These context classes are actually embedded in the parser class, so normally you would refer to them as ExampleParser.ProgContext and ExampleParser.StmtContext and so on.

The ProgContext contains two methods named stmt for accessing the statements that make up the program. Because the occurrence of stmt in the prog grammar rule appears within a star ‘*’ operator, there can be zero or more statements in a program. So you can either call stmt() to retrieve the entire list of them, or use stmt(i) to retrieve the statement at position i (with zero-based indexing, as usual).

The StmtContext includes the method ID() to retrieve the ID token used in an assignment statement, and expr() to return the single expression used in either an assignment or a print statement.

Finally, ExprContext has several of methods for retrieving its components. Because some of the alternatives have two occurrences of expr, the method expr() returns a list, or you can use expr(0) for the first occurrence and expr(1) for the second. The last two alternatives of the expr non-terminal include tokens for numeric literals NUM and variable identifiers ID, so you can access those tokens (a.k.a. TerminalNodes) with NUM() and ID().

Base visitor

In addition to these classes representing nodes in the parse tree, ANTLR generates a visitor class named after the grammar, so in this case, ExampleBaseVisitor. This visitor class includes a distinct method for each non-terminal. So in this case, it contains visitProg, visitStmt, and visitExpr.

The default behavior of these visit methods is to implement a pre-order traversal of the parse tree. Let’s illustrate that by drawing the parse tree that ANTLR generates for the calculator program n=5; print -3*(n+1); as shown in the figure.

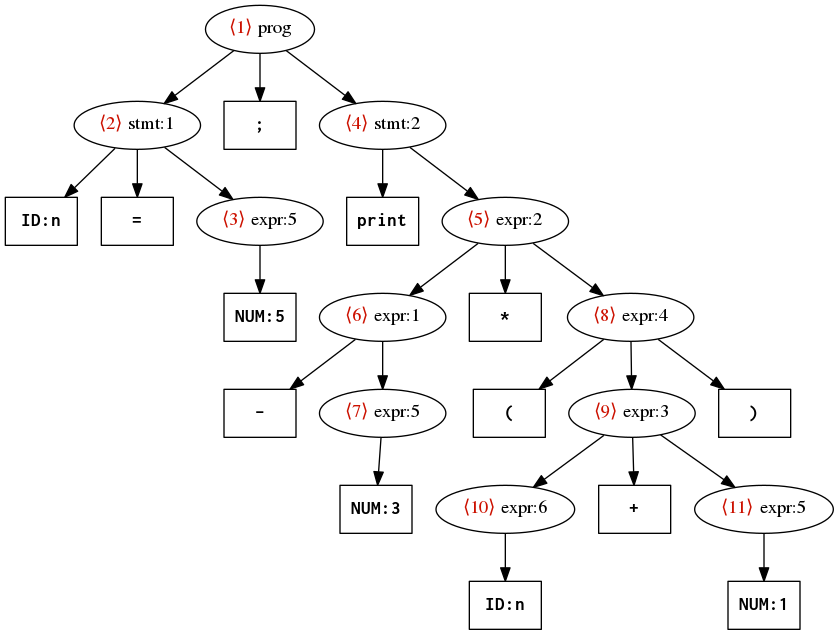
ANTLR parse tree for n=5; print -3*(n+1); The red annotations indicate a pre-order traversal.

To invoke a visitor on a parse tree, we use the method accept(), like this:

ParseTree tree = parser.top();      // or whatever your top-level rule is called
ExampleBaseVisitor visitor = new ExampleBaseVisitor();  // or define a sub-class
top.accept(visitor);                                    // Do the traversal!

When the base visitor is applied to the parse tree above, the following sequence of methods are invoked. Each method call is numbered, and those numbers correspond to the red annotations on the parse tree.

visitProg(ctx) top-level program
- where ctx.stmt(0).getText() is "n=5"
- and ctx.stmt(1).getText() is "print -3*(n+1)"
visitStmt(ctx) assignment statement
- where ctx.ID().getText() is "n"
- and ctx.expr().getText() is "5"
visitExpr(ctx) numeric literal
- where ctx.NUM().getText() is "5"
visitStmt(ctx) print statement
- where ctx.ID() is null
- and ctx.expr().getText() is "-3*(n+1)"
visitExpr(ctx) multiplication
- where ctx.expr(0).getText() is "-3"
- and ctx.expr(1).getText() is "(n+1)"
visitExpr(ctx) negation
- where ctx.expr(0).getText() is "3"
visitExpr(ctx) numeric literal
- where ctx.NUM().getText() is "3"
visitExpr(ctx) parentheses
- where ctx.expr(0).getText() is "n+1"
visitExpr(ctx) addition
- where ctx.expr(0).getText() is "n"
- and ctx.expr(1).getText() is "1"
visitExpr(ctx) variable
- where ctx.ID().getText() is "n"
visitExpr(ctx) numeric literal
- where ctx.NUM().getText() is "1"

By overriding some of these methods in the base visitor, we can determine what happens, including changing the traversal order if we need to.

We also can specify the return types of these methods, because ExampleBaseVisitor takes a type parameter. So if we specify ExampleBaseVisitor<BigInteger> then each visit method will return a BigInteger reference (which could be null). Or we can use regular integer references with ExampleBaseVisitor<Integer>. Or if we don’t need any return type at all, then ExampleBaseVisitor<Void> for which the only valid return value is null. (The reason for Integer rather than int and Void rather than void is that Java generic classes cannot be primitive types, but must be reference types. In practice, the main difference is that reference types can be null.)

Overriding visit methods

Overriding means to substitute a newly-defined method for an existing method in the base visitor.

Let’s say we want to create a visitor that will traverse a parse tree for the calculator language and just keep track of the set of identifiers that are being referenced (assigned or retrieved) in the program.

So in the program illustrated above, n=5; print -3*(n+1); our visitor will just produce the set \(\{\)n\(\}\). But we can imagine more complex programs like a=3; b=z; print c*b+k;. For this one, the set of identifiers would be \(\{\)a, b, c, k, z\(\}\).

To begin this visitor, define a class CollectVarsVisitor that begins like this:

public class CollectVarsVisitor extends ExampleBaseVisitor<Void> {

In order to collect variable names, let’s define a vars field using the Java HashSet type, so it can store a set of strings:

    HashSet<String> vars = new HashSet<String>();

Now, which visit methods do we need to override? Any whose nodes include an ID token — that means visitStmt for the assignment statement and visitExpr for the variable expression. In both cases, ctx.ID() might be null if we’re looking at other alternatives of statements or expressions, so we need to guard against that.

In IntelliJ, we can ask it to fill in the basic structure of an overridden method by selecting Code » Override Methods and then choosing visitStmt and visitExpr. The structure it provides is:

    @Override
    public Void visitStmt(ExampleParser.StmtContext ctx) {
        return super.visitStmt(ctx);
    }

The call to super.visitStmt(ctx) says to jump to the existing implementation of visitStmt in the base class, and execute it. So that falls back to the default traversal behavior. But we can insert some code before or after that super call to take additional actions. Or we can eliminate the super call if we know we don’t need to visit any children of this node.

In order to store all reference variable names into the vars field, we’ll add a bit of logic to visitStmt:

    @Override
    public Void visitStmt(Example1Parser.StmtContext ctx) {
        TerminalNode id = ctx.ID();
        if(id != null) {
            vars.add(id.getText());
        }
        return super.visitStmt(ctx);
    }

So that takes care of all variables that appear on the left side of assignment statements. But what about variables that appear within expressions? Then we need to override visitExpr similarly:

    @Override
    public Void visitExpr(Example1Parser.ExprContext ctx) {
        TerminalNode id = ctx.ID();
        if(id != null) {
            vars.add(id.getText());
        }
        return super.visitExpr(ctx);
    }

Now, after applying the visitor to the parse tree for a=3; b=z; print c*b+k;

        // Setup
        ANTLRInputStream input = new ANTLRInputStream("a=3; b=z; print c*b+k;");
        ExampleLexer lexer = new ExampleLexer(input);
        CommonTokenStream tokens = new CommonTokenStream(lexer);
        ExampleParser parser = new ExampleParser(tokens);
        // Parse and visit
        ParseTree tree = parser.top();
        CollectVarsVisitor visitor = new CollectVarsVisitor();
        tree.accept(visitor);
        // Output result
        System.out.println(visitor.vars);

we get the desired output:

  [b, c, a, k, z]

The ordering of strings in a set is not significant, but this set contains all five variables that are used in the calculator program.

We can achieve all sorts of analyses and translations by overriding methods from the base visitor generated by the ANTLR grammar. But let’s look at two additional tools that make it easier.

Distinguishing rule alternatives

The first tool allows us to put tags or labels on each alternative in the definition of a non-terminal. We do this by placing an identifier next to a pound sign after the definition of the alternative:

stmt : ID '=' expr     #AssignStmt
     | 'print' expr    #PrintStmt
     ;

As before, there are two types of statements, but now they have the explicit labels AssignStmt and PrintStmt. Labeling rules like this allows us to make finer distinctions in the parse tree representation and in the visitor class. Instead of having just one StmtContext class and visitStmt method as before, now ANTLR will generate separate classes and visit methods for each label:

AssignStmtContext class
PrintStmtContext class
visitAssignStmt method
visitPrintStmt method

See the figure for the labeled grammar and the larger set of context classes it generates.

Labeled grammar for calculator language, with corresponding context classes and visitor

Now it is much easier to distinguish between the different node types. Notice that in the expression non-terminal, we used the same label OpExpr for two different alternatives. That works fine, because those alternatives have the same ‘shape’ — they’re both binary operator expressions. We need them to be separate alternatives so we can assign higher precedence to multiplication than to addition. But by naming them both OpExpr we can handle them the same way in the visitor.

The next figure shows the same tree as before, but this time labeled with the explicit rule names rather than the more mysterious expr:2, stmt:2, and the like. Again, the red shows the same pre-order traversal.

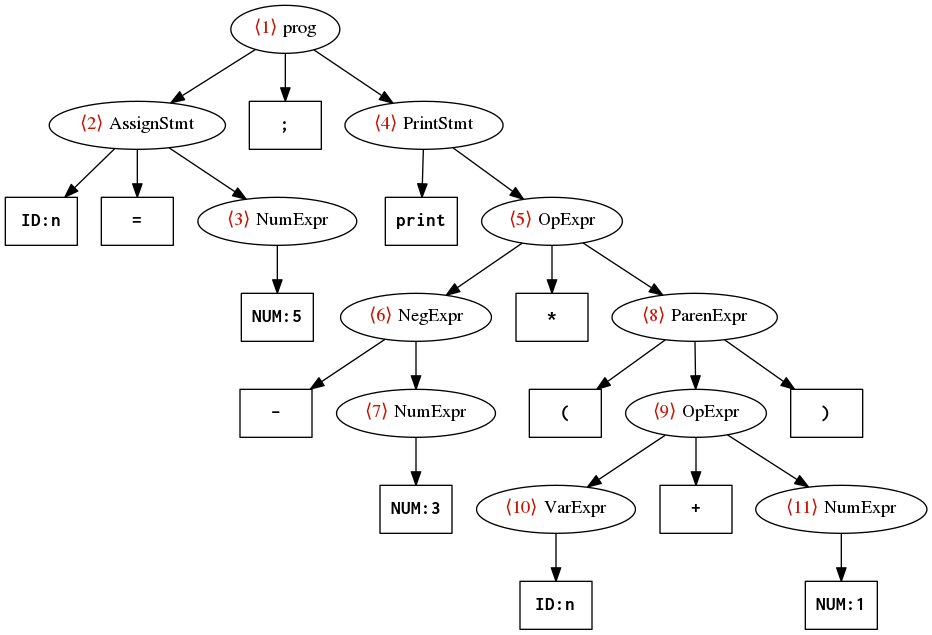
Labeled ANTLR parse tree for n=5; print -3*(n+1);

When the new, expanded base visitor is applied to the new parse tree, the following sequence of methods are invoked. Each method call is numbered, and those numbers correspond to the red annotations on the parse tree.

visitProg(ctx) top-level program
- where ctx.stmt(0).getText() is "n=5"
- and ctx.stmt(1).getText() is "print -3*(n+1)"
visitAssignStmt(ctx) assignment statement
- where ctx.ID().getText() is "n"
- and ctx.expr().getText() is "5"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "5"
visitPrintStmt(ctx) print statement
- where ctx.ID() is null
- and ctx.expr().getText() is "-3*(n+1)"
visitOpExpr(ctx) multiplication
- where ctx.expr(0).getText() is "-3"
- and ctx.expr(1).getText() is "(n+1)"
visitNegExpr(ctx) negation
- where ctx.expr().getText() is "3"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "3"
visitParenExpr(ctx) parentheses
- where ctx.expr().getText() is "n+1"
visitOpExpr(ctx) addition
- where ctx.expr(0).getText() is "n"
- and ctx.expr(1).getText() is "1"
visitVarExpr(ctx) variable
- where ctx.ID().getText() is "n"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "1"

In that sequence of method calls, notice that the ctx.expr method does not always take an integer. Because we can now distinguish negation from parentheses from binary operators, the method types can be more precise. The visitOpExpr requires us to distinguish ctx.expr(0) from ctx.expr(1) because it has two sub-expressions. But for visitNegExpr and visitParenExpr there is just one embedded expression so we can do ctx.expr() (without an index) to retrieve it.

Distinguishing node children

There’s one more distinction we can make in our grammar that can make things a little clearer. Instead of always referring to our children (sub-trees) using non-terminal names and indices like ctx.expr(1), we can give them semantic names. The place this is most useful in the calculator grammar is in the OpExpr alternatives:

expr : '-' expr             #NegExpr
     | left=expr op=('*'|'/') right=expr  #OpExpr
     | left=expr op=('+'|'-') right=expr  #OpExpr
     | '(' expr ')'         #ParenExpr
     | NUM                  #NumExpr
     | ID                   #VarExpr
     ;

Notice the left= and op= and right= preceding each component in OpExpr. These add explicit labels for the children of this node. The expr methods are still available, but now the OpExprContext will have fields with more intuitive names.

OpExprContext class updated with fields for labeled child nodes

I’ll repeat one more time the pre-order traversal of n=5; print -3*(n+1); — this time making use of the field names in each visitOpExpr call:

visitProg(ctx) top-level program
- where ctx.stmt(0).getText() is "n=5"
- and ctx.stmt(1).getText() is "print -3*(n+1)"
visitAssignStmt(ctx) assignment statement
- where ctx.ID().getText() is "n"
- and ctx.expr().getText() is "5"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "5"
visitPrintStmt(ctx) print statement
- where ctx.ID() is null
- and ctx.expr().getText() is "-3*(n+1)"
visitOpExpr(ctx) multiplication
- where ctx.left.getText() is "-3"
- and ctx.op.getText() is "*"
- and ctx.right.getText() is "(n+1)"
visitNegExpr(ctx) negation
- where ctx.expr().getText() is "3"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "3"
visitParenExpr(ctx) parentheses
- where ctx.expr().getText() is "n+1"
visitOpExpr(ctx) addition
- where ctx.left.getText() is "n"
- and ctx.op.getText() is "+"
- and ctx.right.getText() is "1"
visitVarExpr(ctx) variable
- where ctx.ID().getText() is "n"
visitNumExpr(ctx) numeric literal
- where ctx.NUM().getText() is "1"

PDF

Tree visitors

Context classes

Base visitor

Overriding visit methods

Distinguishing rule alternatives

Distinguishing node children