We use the term symbol to refer to any name that is used in a program. A symbol can refer to a type, a function, a variable, a built-in operation, or other things depending on the language. It is more-or-less interchangeable with the term identifier, although sometimes identifier implies that it’s alphanumeric, whereas a symbol could potentially be any sequence of characters. For example, main is both an identifier and a symbol in a C++ program. The operator ++ might be a symbol too, but we don’t necessarily call it an identifier because it’s not alphanumeric.

Scope

In programming languages, the scope of a symbol refers to the portion of a program where that name can be referenced. Here are some examples to help us understand the scope of identifiers in different languages.

C++ example

const int n = 15;
void blip(float i)
{
  char n = floor(i) % 256;
  cout << i << n << endl;
}
int main()
{
  for(int i = 0;
      i < n;
      i++)
  {
    float k = sqrt(i);
    cout << i << blip(k) << endl;
  }
  return 0;
}

Which lines comprise the scope of \(\texttt{n}_1\)?
Which lines comprise the scope of \(\texttt{n}_4\)?
Which lines comprise the scope of \(\texttt{i}_2\)?
Which lines comprise the scope of \(\texttt{i}_9\)?
Which lines comprise the scope of \(\texttt{k}\)?
Which lines comprise the scope of \(\texttt{blip}\)?
Which lines comprise the scope of \(\texttt{main}\)?

SQL example

SELECT *
  FROM product AS p
     , invoice_item AS i
 WHERE i.product_id = p.id;

INSERT INTO product (name, price)
VALUES ('SQL for Dummies', 13.99);

Which lines comprise the scope of p?
Which lines comprise the scope of i?
Which lines comprise the scope of product?

Java

static boolean isEven(int n)
{
    return n == 0 || isOdd(n-1);
}

static boolean isOdd(int n)
{
    return n == 1 || isEven(n-1);
}

Which lines comprise the scope of \(\texttt{n}_1\)?
Which lines comprise the scope of \(\texttt{n}_6\)?
Which lines comprise the scope of \(\texttt{isEven}\)?
Which lines comprise the scope of \(\texttt{isOdd}\)?

Tree structure

In most languages, different scopes can be properly nested within one another — in other words, they form a tree. Here is the same C++ program we examined earlier, but with annotations to indicate where the scope of each symbol begins (‘enter’) and ends (‘leave’).

const int n = 15;
void blip(float i)                 // ENTER n1
{                                  // ENTER blip, i2
  char n = floor(i) % 256;
  cout << i << n << endl;          // ENTER n4
}                                  // LEAVE n4, i2
int main()
{                                  // ENTER main
  for(int i = 0;
      i < n;                       // ENTER i9
      i++)
  {
    float k = sqrt(i);
    cout << i << blip(k) << endl;  // ENTER k
  }                                // LEAVE k, i9
  return 0;
}                                  // LEAVE blip, n1

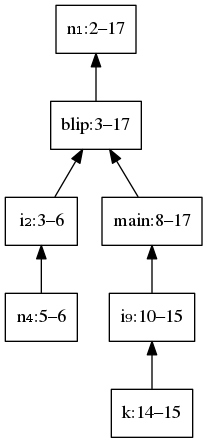
Tree representation of nested scopes in the C++ program.

We never leave one of the outer (parent) scopes without having left its inner (child) scopes. If we did, the enter/leave annotations would look like:

// ENTER a (parent)
// ENTER b (child)
// LEAVE a (parent)
// LEAVE b (child)

Another way to think of properly nested scopes is that they obey a stack discipline. We push child scopes on top of their parents, and then when we leave each scope we pop them last-in first-out (from inner to outer).

Symbol table

In the compiler, we will need a data structure that can track information about a symbol. The most common information we need to track about variables and functions is their types. For example, in the C++ program above we would need to know that \(\texttt{n}_1\) is an integer constant, and \(\texttt{n}_4\) is a character variable.

We may also track other information such as the values of constants, the allocation strategy (where to find this value when we need it), the location of the declaration in the source code, etc.

For simple languages with monolithic scope, (everything is in the same scope), we can just use a standard map implementation, like Java’s HashMap. These tend to be implemented as hash tables or balanced binary trees. In the type-checker for the calculator language, we just used HashMap<String,Type> to map variable names to their types.

But for languages with nested scopes, it’s a little more complex. In addition to methods get and put to (respectively) read and write symbol information, we need to be able to enter and leave scopes. (These are sometimes also called push and pop, as a nod to the stack discipline.)

In the online session, we defined a scope-respecting SymbolTable class that supports methods get, put, enter, and leave. It is defined using a Stack of HashMaps.

PDF

Symbol tables