Formal Language Theory

20 January 2016

Languages and automata

Defining languages

A language is a (possibly infinite) set of strings, where a string is a sequence of symbols (characters) from some alphabet. The alphabet is usually designated by the Greek uppercase \(\Sigma\) (sigma). For example, sequences of binary digits are drawn from \(\Sigma=\{0,1\}\) and base ten integers have \(\Sigma=\{-,0,1,2,3,4,5,6,7,8,9\}\) (the negation sign and all ten numerals).

We can characterize infinite language informally using English descriptions, or by set notation and abusing the ellipses (…), as in these examples:

• \(L_0\) is the set of strings from \(\Sigma=\{a,b\}\) where the sequence \(ab\) is repeated one or more times. E.g., \(L_0 = \{ab, abab, ababab, abababab, \dots\}\) but \(aba\not\in L_0\).

• \(L_1\) is the set of bit strings (from \(\Sigma=\{0,1\}\)) that end in the sequence \(101\). E.g., \(L_1 = \{101, 0101, 1101, 00101, 01101, 10101, 11101, \dots\}\) but \(1010\not\in L_1\).

• \(L_2\) is the set of strings consisting of \(N\) \(a\)’s followed by \(N\) \(b\)’s where \(N \ge 0\). When \(N=0\) this is the empty string, usually designated with the Greek lowercase \(\epsilon\) (epsilon). E.g., \(L_2 = \{\epsilon, ab, aabb, aaabbb, aaaabbbb, \dots\}\) but \(aabbb\not\in L_2\).

• \(L_3\) is the set of base ten representations of natural numbers that are multiples of 3. E.g., \(L_3 = \{0,3,6,9,12,15,18,21,\dots\}\) but \(20\not\in L_3\).

• \(L_4\) is the set of base ten representations of natural numbers that are prime. E.g., \(L_4 = \{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \dots\}\) but \(28 \not\in L_4\).

• \(L_5\) is the set of strings consisting of matched parentheses or brackets. E.g., \(\Sigma=\{\) (, ), [, ] \(\}\) and \(L_5 = \{\epsilon\), (), [], ([]), [()], (()), [[]], ([]()), \(\dots\}\) but ([)] \(\not\in L_5\).

Can we come up with a finite, formal characterization of languages like these? What if we had a well-defined ‘machine’ of some sort that, given any string, can determine whether the string is in the language. In other terms, the machine recognizes or accepts strings in the language, and it rejects any strings not in the language.

Finite State Automata

The type of machine we’ll start with is called a Finite State Automaton (FSA). If the term automaton is unfamiliar, just think of machine or device; the plural form is automata. Below is an example of an FSA for the language \(L_0\).

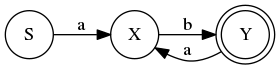
FSA for \(L_0\)

The circles are states, and the arrows are transitions. The state labeled \(S\) is the start state, and the double-circle is an accept or final state. The arrows are labeled with the character that is consumed when you make that transition.

So it works like this: Given a string, let’s say \(abab\), we keep track of what state we’re in and then consume characters one at a time. Each character corresponds to following one of the arrows from the current state. So the first \(a\) moves us from \(S\) to \(X\). The next character is \(b\) so we move from \(X\) to \(Y\). Now we’re in an accept state, so if this was the end of the string, it would be in the language \(L_0\). But since there are more characters we continue. The second \(a\) moves us back to \(X\) and the final \(b\) moves us to \(Y\). We’re back in the accept state and at the end of the string, so the string is recognized by the FSA and therefore it is in the language \(L_0\).

Now, consider some things that can go wrong. What if we encounter a character for which there is no outgoing arrow from the current state? For example, trace the same FSA with the string \(aab\). The first \(a\) takes you to state \(X\), but from there we don’t have an outgoing arrow for the second \(a\). Therefore we’re stuck and the string is rejected: \(aab\not\in L_0\).

Another type of rejection is when we reach the end of the string, but we’re not in the final state. Trace the FSA with the string \(aba\). You’ll get to the end of the string, but end up in state \(X\) which is not a final state. Therefore \(aba\not\in L_0\).

Non-deterministic FSA

Now let’s try to build an FSA for the next sample language, \(L_1\). The simplest way to approach it is to build a non-deterministic FSA. The start state is \(S\), and from there we have self-transitions on \(0\) or \(1\), back to state \(S\). That means we can – at first – have any number of \(0\)’s and \(1\)’s. But to get to the final state \(Z\), we need the string to end with \(101\).

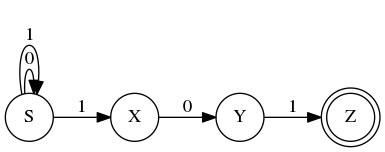
Non-deterministic FSA for \(L_1\)

We can see that the automaton is non-deterministic because, from state \(S\) if we see a \(1\), there are two choices! Do we follow the loop and stay in \(S\), or do we move instead to \(X\)? Consider the string \(1101\). On the first \(1\) if we move to \(X\) then it appears we’re stuck trying to match the second \(1\). The correct way to match this string is to take the loop for the first \(1\) and move to \(X\) on the second \(1\).

The way non-deterministic FSAs are interpreted is that the string is accepted if there is any path that leads to the final state. But when using the machine, how do we know which transitions to take? The strings could be arbitrarily long and complex, so we could have many false starts and have to backtrack.

Fortunately (and maybe surprisingly), any non-deterministic FSA can be converted to a deterministic FSA. The number of states may increase substantially, but it will still be constant relative to the length of the input string.

The conversion algorithm is somewhat intuitive. Starting from the start state, consider each possible input from \(\Sigma\). On a \(0\) we stay in \(S\). But on a \(1\), there are two possibilities: we can end up in either \(S\) or \(X\). So we create a new, union state called \(SX\) and let that be the target of \(1\). Continue from \(SX\): if I’m in either \(S\) or \(X\), what are all the possibilities when I see a \(0\)? Well, if it was \(S\) I would stay put, but if I was in \(X\) I would move to \(Y\). So the new union state is \(SY\). Now, from \(SX\) what are all the possibilities when I see a \(1\)? Well from state \(X\) I would be stuck so I can ignore that. But from state \(S\) I could be in either \(S\) or \(X\). So there is a loop on a \(1\) from \(SX\) to \(SX\).

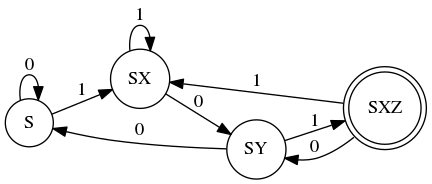
Deterministic FSA for \(L_1\)

Once you consider all possible transitions from these union states, you make any state that includes \(Z\) an accept state – in this example there is just one, but it’s possible the non-deterministic accept state could be a member of multiple deterministic union states.

Implementing FSAs

It’s straightforward to implement a deterministic FSA in any programming language. Just keep track of the state and loop through the characters. Here is a Java program that implements the FSA for \(L_0\).

public class FSA_L0 {
    enum State { S, X, Y };

    static boolean runFSA(String buffer) {
        State state = State.S;  // Start state
        for(int position = 0; position < buffer.length(); position++) {
            char current = buffer.charAt(position);
            switch(state) {
            case S:
                if('a' == current) state = State.X;
                else return false; // Stuck
                break;
            case X:
                if('b' == current) state = State.Y;
                else return false; // Stuck
                break;
            case Y:
                if('a' == current) state = State.X;
                else return false; // Stuck
                break;
            }
        }
        return state == State.Y; // Are we in accept state?
    }

    public static void main(String[] args) {
        if(args.length > 0) {   // Try strings provided on command line
            for(String arg : args) {
                System.out.println
                    ((runFSA(arg)? "ACCEPT" : "REJECT") + ": " + arg);
            }
        }
        else {                  // Built-in test cases
            assert(runFSA("ab"));
            assert(runFSA("abab"));
            assert(runFSA("ababab"));
            assert(!runFSA("a"));
            assert(!runFSA(""));
            assert(!runFSA("aba"));
            assert(!runFSA("baba"));
            System.out.println("Tests pass.");
        }
    }
}

We invoke it like this:

% java FSA_L0 ab abc abb aba abab
ACCEPT: ab
REJECT: abc
REJECT: abb
REJECT: aba
ACCEPT: abab

% java FSA_L0
Tests pass.

Exercises

1. Create a non-deterministic FSA to recognize the language \(L_6\), the set of strings from \(\Sigma=\{a,b,n\}\) that begin with \(ba\) and end with \(na\). For example, it should accept \(bana\), \(banana\), \(babbna\) but not \(banba\).

2. Convert the non-deterministic FSA from the previous exercise into a deterministic FSA. Try it on the same strings.

3. Create a deterministic FSA to recognize the language \(L_3\), the natural numbers that are multiples of \(3\). I’ve provided an incomplete starting point below that accepts \(\{0,3,6,9,12,15,18,21\}\). As a shorthand, I’ve labeled arrows with more than one digit to indicate that any of those digits will follow that arrow. You should expand the given FSA so it works for any number in the infinite set \(L_3\). Surprisingly, you shouldn’t need more states, just more arrows. One observation that makes this possible is that the sum of the digits of a number that is a multiple of 3 is also a multiple of 3. So we can tell that 236,529 is a multiple of 3 because \(2+3+6+5+2+9=27\) and 27 is a multiple of 3. (Which we can, in turn, tell because \(2+7=9\) is a multiple of 3.)

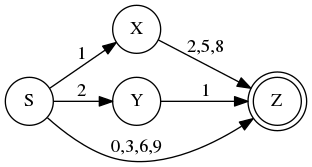
Incomplete FSA for \(L_3\) and exercise 3

4. Using the same technique as in the Java program above, implement your deterministic FSA from exercise 2. (You can use Java or C/C++.)

Chomsky Hierarchy

When we try to create an FSA for \(L_2\), we run into trouble. Recall that \(L_2\) requires a sequence of \(a\)’s followed by a sequence of \(b\)’s, but those sequences must have the same length. So \(aabb\in L_2\) but \(aaabb\not\in L_2\). We can design an FSA that requires a sequence of \(a\)’s followed by a sequence of \(b\)’s, but it won’t be able to count that we’re getting the same number of \(a\)’s and \(b\)’s.

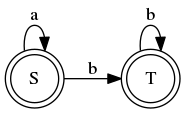
Candidate FSA for \(L_2\) (doesn’t work)

The candidate FSA accepts everything in \(L_2\), but it fails to reject some strings that are not in \(L_2\), such as \(aaabb\).

Because strings in the language can be arbitrarily long, we cannot keep track of lengths using a constant number of states. There is an expansion of FSAs called push-down automata (PDA) that addresses this problem. In addition to the states and transitions, push-down automata use a stack where you can push or pop data on each transition. So if we push each \(a\) as we encounter it, then when we transition to \(b\)’s we can pop an \(a\) for each \(b\). If the stack is empty when we get to the end of the string, then the counts matched.

PDAs are strictly more powerful than FSAs – they can recognize more languages. In this way, definable languages can be placed into a hierarchy based on the power of the machine needed to recognize them. This is called the Chomsky Hierarchy, after linguist Noam Chomsky described it in his book Syntactic Structures in 1957.

• Type 0 = Recursively enumerable languages, recognizable by Turing Machine
• Type 1 = Context-sensitive languages, recognizable by a linear-bounded automaton
• Type 2 = Context-free languages, recognizable by PDA
• Type 3 = Regular languages, recognizable by FSA

Types 2 and 3 are of the most interest to us, in studying programming languages and compilers. Programming languages are usually defined to be context-free, and tokens (like a number, string, or identifier) are regular.

Regular expressions

Regular languages show up in many computer programs in the form of regular expressions, also known as regexes. A regular expression is a type of pattern that can be used to search or match text. They are essential to the command-line tool grep and built in to the syntax of languages like Perl and Javascript.

We won’t cover regular expressions in great detail here, but suffice to say that a dot . matches any single character, a * is a post-fix operator that matches zero or more occurrences of the preceding character or group, and [abc] matches any single character from the set \(\{a,b,c\}\). So the regular expression c.lo*[rn] would match colr, colon, color, coloon, calr, calon, czloooor but not colour or caloot.

The set of strings matched by a regular expression forms a regular language. Therefore any regular expression can be translated to an FSA, and in fact this is often how they are implemented. Supposing that \(\Sigma=\{a,b,c,\dots,z\}\), here is an FSA that matches c.lo*[rn]. The \(\Sigma\) label on one of the arrows means you can make that transition on any character in \(\Sigma\).

FSA for the regular expression c.lo*[rn]

Exercises

5. Convert the regular expression [cdf]([aoeui][tgr])* to an FSA. As in arithmetic, the parentheses group together elements of the regex so the * operator applies to the whole group. Some strings that match this expression are c, cat, dog, dig, cator, cigar, firet, caterer, and forager.

Grammars

Another tool for characterizing languages is a grammar. The common notation is called Backus-Naur Form (BNF) named after the early programming language developers John Backus and Peter Naur. A grammar consists of a set of terminals and non-terminals, and production rules that determine how sequences of them can be transformed into other sequences. In the treatment below, we’ll use lowercase letters for terminals and uppercase for non-terminals, but other typographical treatments are sometimes used too.

This is a grammar for a subset of simple English sentences. The non-terminal S stands for sentence, but it’s also the starting rule. Read the bar character | as “or” – it introduces an alternative to the rule above.

S    ::= NP VP

NP   ::= NOUN
       | ADJ NP

VP   ::= VERB
       | VP ADV

NOUN ::= dog
       | idea
       | pizza

ADJ  ::= green
       | mean
       | tasty

VERB ::= sleeps
       | eats
       | learns

ADV  ::= furiously
       | studiously
       | quickly

The above grammar can be used to generate all sorts of strange quasi-English sentences, like “tasty green pizza learns quickly” and “mean dog sleeps.”

To generate a sentence, start with an S and then expand it using any of the available rules where S appears on the left side of ::=. There is only one, so the first layer transforms S into NP VP. Now, for NP there are two choices – do we want some adjectives or just a noun by itself? As you continue expanding non-terminals, the process naturally constructs a tree where the leaves are the terminals in your final sentence.

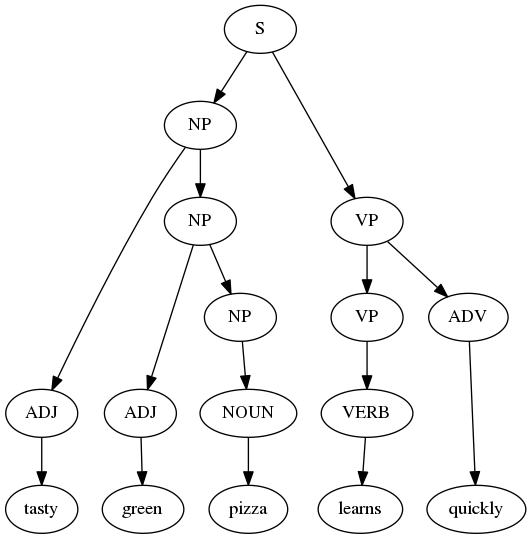
Parse tree for an English sentence

The inverse problem is called parsing. That is, given a sentence that we suspect is in the language, what grammar rules would be invoked to generate that sentence? Or in other terms, given the sentence how do we construct the tree?

Let’s try to create a grammar to characterize the language \(L_2\), which we learned was not regular. Its strings contain a sequence of a’s followed by the same number of b’s. The grammar is actually quite simple.

S ::= ε
    | aSb

The start non-terminal S can either transform to an empty string, or it can recursively become an S surrounded by an a on the left and a matching b on the right. This ensures we generate the same number of as as bs.

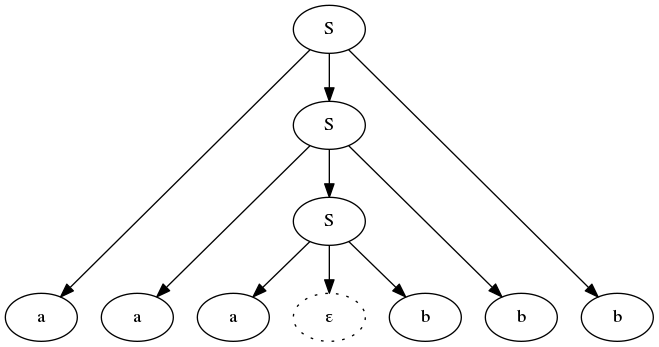
Parse tree for the \(L_2\) string aaabbb

The grammars above are context-free. You can easily tell this because the left-hand side of each ::= is just a single non-terminal. If we allow terminals on either side of the non-terminal (all on the left side of ::=), then the rule can only be applied when in a matching context, so the grammar is context-sensitive.

Here’s a small example of a context-sensitive grammar. It recognizes a language from \(\Sigma=\{a,b,c\}\) where there are sequences of \(a\)s, then \(b\)s, and then \(c\)s all with the same number of characters.

S  ::= aSBc     (rule 1)
     | abc           (2)
cB ::= Bc            (3)
bB ::= bb            (4)

Notice how the left side of the ::= in two of the rules contains a terminal. That means the B can only be expanded one way if there is a c to its left, and a different way if there is a b to its left. Below is a derivation that generates a string in the language.

S ⇒ aSBc     (rule 1)
  ⇒ aaSBcBc       (1)
  ⇒ aaabcBcBc     (2)
  ⇒ aaabBccBc     (3)
  ⇒ aaabbccBc     (4)
  ⇒ aaabbcBcc     (3)
  ⇒ aaabbBccc     (3)
  ⇒ aaabbbccc     (4)

Exercises

6. Using the English-like grammar above, draw the parse tree for the sentence “mean idea eats furiously quickly.”

7. The English-like grammar doesn’t support subject-verb agreement. Suppose we wish to add plural nouns like dogs/ideas/pizzas and plural verbs like sleep/eat/learn. Revise and extend the grammar to ensure subject-verb agreement, so that “dogs eat” and “dog eats” are in the language, but not “dogs eats” or “dog eat”. Your grammar should continue to support the same adjectives and adverbs.

8. Write a context-free grammar corresponding to the language \(L_5\) consisting of strings of matched parentheses. Using your grammar, draw the parse tree for ([]()).